
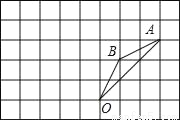
如图所示,在边长为1的正方形组成的网格中,△AOB的顶点均在格点上,点A,B的坐标分别是A(3,3)、B(1,2),△AOB绕点O逆时针旋转90°后得到△A1OB1.
(1)画出△A1OB1,直接写出点A1,B1的坐标;
(2)在旋转过程中,点B经过的路径的长.
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:初中数学 来源:2017年广东省河源市中考数学一诊试卷 题型:解答题
先化简,再求值: 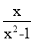 ÷(1+
÷(1+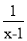 ),其中x=
),其中x=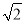 ﹣1.
﹣1.
查看答案和解析>>
科目:初中数学 来源:北京四中2018届上学期初中九年级期中考试数学试卷 题型:解答题
问题探究:
新定义:
将一个平面图形分为面积相等的两部分的直线叫做该平面图形的“等积线”,其“等积线”被该平面图形截得的线段叫做该平面图形的“等积线段”(例如圆的直径就是圆的“等积线段”)
解决问题:
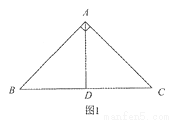
已知在Rt△ABC中,∠BAC=90°,AB=AC=2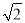 .
.
(1)如图1,若AD⊥BC,垂足为D,则AD是△ABC的一条等积线段,直接写出AD的长;
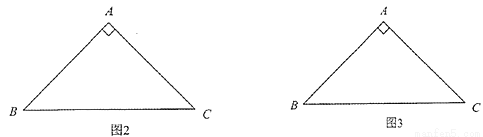
(2)在图2和图3中,分别画出一条等积线段,并直接写出它们的长度. (要求:图1、图2和图3中的等积线段的长度各不相等)
查看答案和解析>>
科目:初中数学 来源:北京四中2018届上学期初中九年级期中考试数学试卷 题型:单选题
如图,D,E为△ABC的边AB,AC上的点,DE∥BC,若AD:DB=1:3,AE=2,则AC的长是( ).
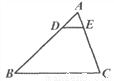
A. 10 B. 8 C. 6 D. 4
B 【解析】∵DE//BC, ∴AE:EC=AD:DB, ∵AD:DB=1:3, ∴AE:EC=1:3, ∵AE=2,∴EC=6, ∴AC=AE+EC=8, 故选B.查看答案和解析>>
科目:初中数学 来源:2017年甘肃省张掖市中考数学三模试卷 题型:解答题
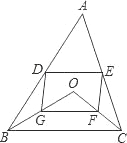
D、E分别是不等边三角形ABC(即AB≠BC≠AC)的边AB、AC的中点.O是△ABC所在平面上的动点,连接OB、OC,点G、F分别是OB、OC的中点,顺次连接点D、G、F、E.
(1)如图,当点O在△ABC的内部时,求证:四边形DGFE是平行四边形;
(2)若四边形DGFE是菱形,则OA与BC应满足怎样的数量关系?(直接写出答案,不需要说明理由.)
查看答案和解析>>
科目:初中数学 来源:2017年甘肃省张掖市中考数学三模试卷 题型:填空题
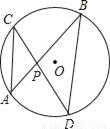
如图,在⊙O中,弦AB,CD相交于点P.若∠A=40°,∠APD=75°,则∠B= .
查看答案和解析>>
科目:初中数学 来源:2017年甘肃省张掖市中考数学三模试卷 题型:单选题
抛物线y=ax2+bx+c(a≠0)的图象如图所示,则下列说法正确的是( )
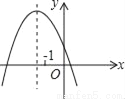
A. b2﹣4ac<0 B. abc<0 C. 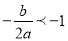 D. a﹣b+c<0
D. a﹣b+c<0
查看答案和解析>>
科目:初中数学 来源:2017年福建省分校九年级数学综合试卷(二) 题型:填空题
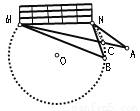
如图,在足球比赛场上,甲、乙两名队员互相配合向对方球门MN进攻,当甲带球冲到A点时,乙也跟随冲到B点.从数学角度看,此时甲是自己射门好,还是将球传给乙,让乙射门好?
答________________.
查看答案和解析>>
科目:初中数学 来源:2017年黑龙江省大庆市中考数学三模试卷 题型:解答题
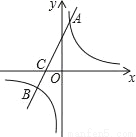
如图,在平面直角坐标系中,一次函数y=kx+b(k≠0)的图象与反比例函数y=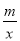 (m≠0)的图象交于A、B两点,与x轴交于C点,点A的坐标为(n,6),点C的坐标为(﹣2,0),且tan∠ACO=2.
(m≠0)的图象交于A、B两点,与x轴交于C点,点A的坐标为(n,6),点C的坐标为(﹣2,0),且tan∠ACO=2.
(1)求该反比例函数和一次函数的解析式;
(2)求点B的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com