练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    2016年元旦期间日月峡水伊方优惠开放．门票售价为：成人票每张150元，儿童票每张70元．如果某日水伊方售出门票100张，门票收入共11000元．那么当日售出成人票________张．

    50 【解析】根据题意，设当日售出成人票x张，则儿童票可表示为（100﹣x）张，由于成人票每张150元，儿童票每张70元，则利用门票收入列方程得150x+70（100﹣x）=11000，然后解得x=50． 故答案为：50．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：江苏省无锡市2018届九年级12月月考数学试卷 题型：填空题

    二次函数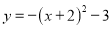的顶点坐标是_______.

    （-2，-3） 【解析】试题分析：二次函数y＝－(x＋2)2－3是顶点式， ∴二次函数y＝－(x＋2)2－3的顶点坐标是：（－2，－3）． 故答案为：（－2，－3）．

    查看答案和解析>>

    科目：初中数学 来源：山东省滨州市无棣县2018届九年级（上）期中数学试卷（解析版） 题型：填空题

    已知关于x的一元二次方程ax2﹣2x﹣1=0有两个不相等的实数根，则a的取值范围是__________

    a＞﹣1且a≠0 【解析】∵关于的一元二次方程有两个不相等的实数根， ∴ ，解得： 且. 即的取值范围是： 且.

    查看答案和解析>>

    科目：初中数学 来源：浙江省宁波市2017-2018学年七年级上册期末模拟数学试卷 题型：解答题

    如图所示，点C、D为线段AB的三等分点，点E为线段AC的中点，若ED=9，求线段AB的长度．

    18. 【解析】 试题分析：理解线段的中点及三分点的概念，灵活运用线段的和、差、倍、分转化线段之间的数量关系． 试题解析：∵C、D为线段AB的三等分点， ∴AC=CD=DB 又∵点E为AC的中点，则AE=EC=AC ∴CD+EC=DB+AE ∵ED=EC+CD=9 ∴DB+AE=EC+CD=ED=9， 则AB=2ED=18．

    查看答案和解析>>

    科目：初中数学 来源：浙江省宁波市2017-2018学年七年级上册期末模拟数学试卷 题型：填空题

    单项式﹣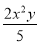的系数是________，次数是________

    - 3 【解析】根据单项式定义得：单项式﹣的系数是﹣， 次数是3． 故答案为： ，3.

    查看答案和解析>>

    科目：初中数学 来源：浙江省宁波市2017-2018学年七年级上册期末模拟数学试卷 题型：单选题

    如图，∠ABC=∠ACB，AD、BD、CD分别平分△ABC的外角∠EAC、内角∠ABC、外角∠ACF．以下结论：①AD∥BC；②∠ACB=2∠ADB；③∠ADC+∠ABD=90°；④∠BDC=∠BAC．其中正确的结论有（　　）

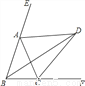
    A. 1个 B. 2个 C. 3个 D. 4个

    C 【解析】①∵AD平分△ABC的外角∠EAC， ∴∠EAD=∠DAC， ∵∠EAC=∠ACB+∠ABC，且∠ABC=∠ACB， ∴∠EAD=∠ABC， ∴AD∥BC， 故①正确。 ②由(1)可知AD∥BC， ∴∠ADB=∠DBC， ∵BD平分∠ABC， ∴∠ABD=∠DBC， ∴∠ABC=2∠ADB， ∵∠ABC=∠ACB，...

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年第一学期期末复习备考之精准复习模拟题七年级人教版数学试卷（C卷） 题型：解答题

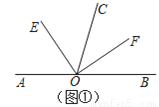
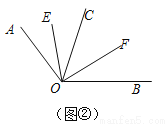
    下列各小题中，都有OE平分∠AOC，OF平分∠BOC．

    （1）如图①，若点A、O、B在一条直线上，∠EOF= ；

    （2）如图②，若点A、O、B不在一条直线上，∠AOB=140°，则∠EOF= ；

    （3）由以上两个问题发现：当∠AOC在∠BOC的外部时，∠EOF与∠AOB的数量关系是∠EOF= ；

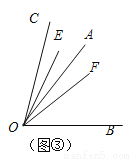
    （4）如图③，若OA在∠BOC的内部，∠AOB和∠EOF还存在上述的数量关系吗？请简单说明理由；

    （1）90°；（2）70°；（3）∠AOB；（4）存在． 【解析】试题分析：（1）根据OE平分∠AOC，OF平分∠BOC，点A、O、B在一条直线上，即可得到∠EOF的度数； （2）根据OE平分∠AOC，OF平分∠BOC，∠AOB=140°，即可得到∠EOF的度数； （3）根据（2）中的方法，即可得到∠EOF与∠AOB的数量关系； （4）若OA在∠BOC的内部，∠AOB和∠E...

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年第一学期期末复习备考之精准复习模拟题七年级人教版数学试卷（C卷） 题型：单选题

    如图，M，N，P，R分别是数轴上四个整数所对应的点，其中有一点是原点，并且这四个整数点每相邻两点之间的距离为1个单位长度.数a对应的点在M与N之间，数b对应的点在P与R之间，若|a|+|b|=3，则原点是（　　）

    A. M或N B. N或P C. P或R D. M或R

    D 【解析】试题解析：【解析】 设数a对应的点为A，数b对应的点为B． ∵MN=NP=PR=1，∴|MN|=|NP|=|PR|=1，∴|MR|=3； ①当原点在N或P点时，|a|+|b|＜3，因为|a|+|b|=3，所以原点不可能在N或P点； ②当原点在M、R时且|MA|=|BR|时，|a|+|b|=3； 综上所述，此原点应是在M或R点． 故选D．

    查看答案和解析>>

    科目：初中数学 来源：2017年海南省中考数学模拟试卷（三） 题型：单选题

    如图，在△ABC、△ADE中，C、D两点分别在AE、AB上，BC、DE交于点F，若BD=DC=CE，∠ADC+∠ACD=114°，则∠DFC为（ ）

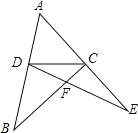
    A．114° B．123° C．132° D．147°

    B． 【解析】 试题分析：∵BD=CD=CE，等腰三角形的性质得出∠B=∠DCB，∠E=∠CDE， ∵∠ADC+∠ACD=114°，∴∠BDC+∠ECD=360°﹣114°=246°， ∴∠B+∠DCB+∠E+∠CDE=360°﹣246°=114°， ∴∠DCB+∠CDE=57°， ∴∠DFC=180°﹣57°=123°， 故选B．

    查看答案和解析>>

    同步练习册答案