
6����ͼ1�ij�Ϊa����Ϊb��a��b����С������ֽƬ����ͼ2��ʽ���ص��ط��ھ���ABCD�ڣ�δ�����ǵIJ��֣��������Σ�����Ӱ��ʾ�������Ͻ������½ǵ���Ӱ���ֵ�����IJ�ΪS����BC�ij��ȱ仯ʱ������ͬ���ķ��÷�ʽ��Sʼ�ձ��ֲ��䣬��a��b���㣨 ��
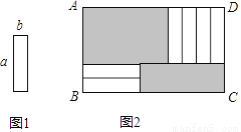
A. a=2b B. a=3b C. a=4b D. a=b
A �������������������ͼ�� ���Ͻ���Ӱ���ֵij�ΪAE����ΪAF=3b�����½���Ӱ���ֵij�ΪPC����Ϊa�� ��AD=BC����AE+ED=AE+a��BC=BP+PC=4b+PC�� ��AE+a=4b+PC����AE-PC=4b-a�� ����Ӱ�������֮��S=AE•AF-PC•CG=3bAE-aPC=3b��PC+4b-a��-aPC=��3b-a��PC+12b2-3ab�� ��3b-a=0����...
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ���˽̰���꼶�²���ѧ ��19�� һ�κ��� ��Ԫ���� ���ͣ������
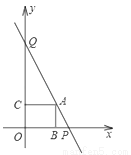
��ͼ��ֱ��y=��2x+8����������ֱ���P��Q���㣬���߶�PQ����һ��A����A��ֱ�����������Ĵ��ߣ�����ֱ�ΪB��C��
��1��������ABOC�����Ϊ5����A�����꣮
��2������A���߶�PQ���ƶ��������ABOC��������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���˽̰����꼶�²���ѧ �ھ��� ����ʽ�벻��ʽ�� ��Ԫ���� ���ͣ���ѡ��
�������ʽ��a+1��x��a+1�Ľ⼯Ϊx��1����ôa��ȡֵ��Χ�ǣ�������
A. a��1 B. a����1 C. a��1 D. a����1
B ����������a+1��x��a+1�� ��a+1��0ʱx��1�� ����a+1��0�����a��-1�� ��ѡ��B���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ����ʦ������꼶�²���ѧ ��һ�� ��ʽ�ij˳� ��Ԫ���� ���ͣ������
���3m=6��3n=2����ô3m��nΪ��________
3 ����������3m=6��3n=2�� ��3m��n=3m��3n=6��2=3�� �ʴ�Ϊ��3.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ����ʦ������꼶�²���ѧ ��һ�� ��ʽ�ij˳� ��Ԫ���� ���ͣ���ѡ��
����100m•1000n�Ľ���ǣ� ��
A. 100000m+n B. 100mn C. 1000mn D. 102m+3n
D ��������100m•1000n=��102��m��(103)n=102m��103n=102m+3n�� ��ѡD.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ����ʦ������꼶�²���ѧ ��һ�� ��ʽ�ij˳� ��Ԫ���� ���ͣ���ѡ��
��֪4y2+my+9����ȫƽ��ʽ����mΪ�� ��
A. 6 B. ��6 C. ��12 D. 12
C ����������Ϊ4y2=(2y)2��9=32������my=��2��2y��3=��12y��m=��12�� ��ѡC.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���˽̰���꼶�²���ѧ ��28�� ������Ǻ��� ��Ԫ���� ���ͣ������
��֪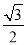 ��cosA��sin70�㣬�����A��ȡֵ��Χ�� ��
��cosA��sin70�㣬�����A��ȡֵ��Χ�� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���˽̰���꼶�²���ѧ ��28�� ������Ǻ��� ��Ԫ���� ���ͣ���ѡ��
��ͼ���ӵ̺����ӭˮ��AB���±���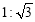 ���̸�BC=10m��������AB�ij����ǣ� ��
���̸�BC=10m��������AB�ij����ǣ� ��
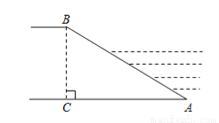
A��15m B��20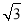 m
m
C��20m D��10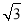 m
m
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���㽭������ɽ��2016-2017ѧ����꼶��ѧ����ĩ��ѧ�Ծ� ���ͣ���ѡ��
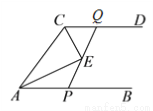
��ͼ������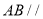 ����
����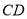 ��
�� 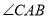 ��
��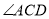 ��ƽ���߽��ڵ�
��ƽ���߽��ڵ�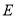 ��
�� 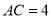 ����
����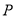 ������
������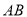 �ϵ�һ���㣬����
�ϵ�һ���㣬����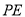 ���ӳ�������
���ӳ�������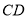 �ڵ�
�ڵ�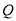 ���������н��ۣ���
���������н��ۣ���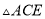 ��ֱ�������Σ���
��ֱ�������Σ���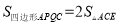 ������
������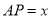 ��
�� 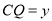 ����
����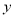 ����
����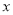 �ĺ�������ʽ��
�ĺ�������ʽ��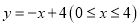 ��������ȷ���ǣ� ����
��������ȷ���ǣ� ����
A. �٢ڢ� B. �٢� C. �٢� D. �ڢ�
A ������������ƽ���ߵ����ʼ���ƽ���ߵĶ����֤����ȷ������ȡ�㣬ʹ��ͨ��֤����ռ���֤���ڢ���ȷ. �������� �ߣ� �࣬ �֡����ƽ���߽��ڵ㣬 �࣬ �࣬ ����ֱ�������Σ� �����ȷ�� ����ȡ�㣬ʹ�� �����У� �ߣ� ��գ� �࣬ �� �֡ߣ� �࣬ �࣬ �֡ߣ� �� ��գ� �࣬...�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com