
计算100m•1000n的结果是( )
A. 100000m+n B. 100mn C. 1000mn D. 102m+3n
D 【解析】100m•1000n=(102)m·(103)n=102m·103n=102m+3n, 故选D.科目:初中数学 来源:北师大版八年级下册数学 第一章 三角形的证明 单元检测卷 题型:单选题
已知等腰三角形的两边长是5cm和6cm,则此三角形的周长是( )
A.16cm B.17cm C.11cm D.16cm或17cm
D 【解析】 试题分析:当5为腰长时,则等腰三角形的周长为:5×2+6=16cm;当6为腰长时,则等腰三角形的周长为:6×2+5=17cm.查看答案和解析>>
科目:初中数学 来源:人教版七年级下册数学 第九章 不等式与不等式组 单元检测卷 题型:单选题
若a<0关于x的不等式ax+1>0的解集是( )
A.x>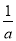 B.x<
B.x<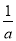 C.x>-
C.x>-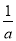 D.x<-
D.x<-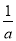
查看答案和解析>>
科目:初中数学 来源:北师大版七年级下册数学 第一章 整式的乘除 单元检测卷 题型:解答题
已知一个长方形的面积为(6x2y+12xy﹣24xy3 )平方厘米,它的宽为6xy厘米,求它的长为多少厘米?
(x+2﹣4y2)厘米. 【解析】试题分析:利用矩形面积公式,结合整式的除法运算法则求出答案. 试题解析:∵一个长方形的面积为(6x2y+12xy﹣24xy3 )平方厘米,它的宽为6xy厘米, ∴它的长为:(6x2y+12xy﹣24xy3 )÷6xy=(x+2﹣4y2)厘米.查看答案和解析>>
科目:初中数学 来源:北师大版七年级下册数学 第一章 整式的乘除 单元检测卷 题型:填空题
(﹣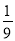 )﹣1=________; (﹣
)﹣1=________; (﹣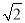 )﹣2=________;(﹣0.1)﹣2=________.
)﹣2=________;(﹣0.1)﹣2=________.
查看答案和解析>>
科目:初中数学 来源:北师大版七年级下册数学 第一章 整式的乘除 单元检测卷 题型:单选题
6张如图1的长为a,宽为b(a>b)的小长方形纸片,按图2方式不重叠地放在矩形ABCD内,未被覆盖的部分(两个矩形)用阴影表示.设左上角与右下角的阴影部分的面积的差为S,当BC的长度变化时,按照同样的放置方式,S始终保持不变,则a,b满足( )
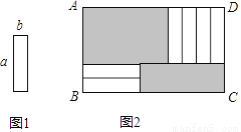
A. a=2b B. a=3b C. a=4b D. a=b
A 【解析】试题解析:如图, 左上角阴影部分的长为AE,宽为AF=3b,右下角阴影部分的长为PC,宽为a, ∵AD=BC,即AE+ED=AE+a,BC=BP+PC=4b+PC, ∴AE+a=4b+PC,即AE-PC=4b-a, ∴阴影部分面积之差S=AE•AF-PC•CG=3bAE-aPC=3b(PC+4b-a)-aPC=(3b-a)PC+12b2-3ab, 则3b-a=0,即...查看答案和解析>>
科目:初中数学 来源:人教版九年级下册数学 第28章 锐角三角函数 单元检测卷 题型:解答题
如图,是某广场台阶(结合轮椅专用坡道)景观设计的模型,以及该设计第一层的截面图,第一层有十级台阶,每级台阶的高为0.15米,宽为0.4米,轮椅专用坡道AB的顶端有一个宽2米的水平面BC;《城市道路与建筑物无障碍设计规范》第17条,新建轮椅专用坡道在不同坡度的情况下,坡道高度应符合以下表中的规定:
坡度 | 1:20 | 1:16 | 1:12 |
最大高度(米) | 1.50 | 1.00 | 0.75 |
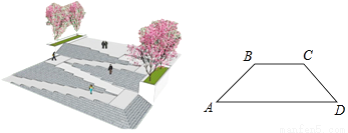
(1)选择哪个坡度建设轮椅专用坡道AB是符合要求的?说明理由;
(2)求斜坡底部点A与台阶底部点D的水平距离AD.
斜坡底部点A与台阶底部点D的水平距离AD为62米 【解析】试题分析:(1)计算最大高度为:0.15×10=1.5(米),由表格查对应的坡度即可做出判断; (2)作梯形的高BE、CF,由坡度计算出AE、DF的长,相加即可得AD的长. 试题解析:(1)∵第一层有十级台阶,每级台阶的高为0.15米, ∴最大高度为0.15×10=1.5(米), 由表知建设轮椅专用坡道AB选择...查看答案和解析>>
科目:初中数学 来源:人教版九年级下册数学 第28章 锐角三角函数 单元检测卷 题型:单选题
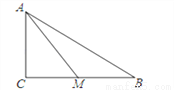
如图,在Rt△ABC中,∠C=90°,AM是BC边上的中线,sin∠CAM=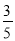 ,则tanB的值为( )
,则tanB的值为( )
A. 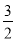 B.
B. 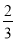 C.
C. 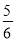 D.
D. 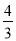
查看答案和解析>>
科目:初中数学 来源:浙江杭州萧山区2016-2017学年八年级上学期期末数学试卷 题型:填空题
已知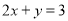 ,且
,且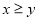 .
.
(1)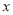 的取值范围是__________;
的取值范围是__________;
(2)若设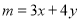 ,则
,则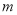 的最大值是__________.
的最大值是__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com