
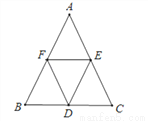
如图,点D、E、F分别是△ABC三边的中点,且AB=AC,则图中的四边形________ 是菱形.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:北师大版九年级下册数学全册综合测试卷二 题型:填空题
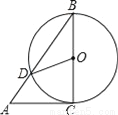
如图,AC是⊙O的切线,切点为C,BC是⊙O的直径,AB交⊙O于点D,连接OD,若∠A=50°,则∠COD的度数为_____.
查看答案和解析>>
科目:初中数学 来源:北师大版九年级下册数学全册综合测试卷一 题型:填空题
在平面直角坐标系中,将函数y=﹣2x2的图象先向右平移1个单位长度,再向上平移5个单位长度,所得图象的函数表达式是 .
y=2(x﹣1)2+5. 【解析】试题分析:由“左加右减”的原则可知,抛物线y=﹣2x2的图象向右平移1个单位所得函数图象的关系式是:y=﹣2(x﹣1)2; 由“上加下减”的原则可知,抛物线y=﹣2(x﹣1)2的图象向上平移5个单位长度所得函数图象的关系式是:y=2(x﹣1)2+5.查看答案和解析>>
科目:初中数学 来源:北师大版九年级下册数学全册综合测试卷一 题型:单选题
一个直角三角形有两条边长为3,4,则较小的锐角约为( )
A. 37° B. 41° C. 37°或41° D. 以上答案均不对
C 【解析】试题解析:①若3、4是直角边, ∵两直角边为3,4, ∴斜边长==5, ∴较小的锐角所对的直角边为3,则其正弦值为; ②若斜边长为4,则较小边=≈2.65, ∴较小边所对锐角正弦值约==0.6625, 利用计算器求得角约为37°或41°. 故选C.查看答案和解析>>
科目:初中数学 来源:人教版八年级下册数学全册综合测试二 题型:填空题
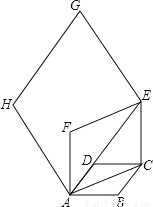
如图,边长为1的菱形ABCD中,∠DAB=60°.连结对角线AC,以AC为边作第二个菱形ACEF,使∠FAC=60°.连结AE,再以AE为边作第三个菱形AEGH使∠HAE=60°…按此规律所作的第n个菱形的边长是_______.
查看答案和解析>>
科目:初中数学 来源:人教版八年级下册数学全册综合测试二 题型:单选题
如图,在菱形ABCD中,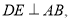 垂足是点E,
垂足是点E, 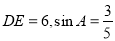 ,则菱形ABCD的周长是( )
,则菱形ABCD的周长是( )

A.20 B.30 C. 40 D.50
C 【解析】分析:DE⊥AB于B,DE=6,sinA= ,可以得出AD的长度,又四边形ABCD菱形,故菱形ABCD的周长为4AD. 解答:【解析】 根据题意,DE⊥AB于B,DE=6,sinA=, 所以AD==10, 又因为四边形ABCD菱形, 故周长为40. 故选C.查看答案和解析>>
科目:初中数学 来源:人教版八年级下册数学全册综合测试二 题型:单选题
学校为了丰富学生课余活动开展了一次“爱我学校,唱我学校”的歌咏比赛,共有18名同学入围,他们的决赛成绩如下表:
成绩(分) | 9.40 | 9.50 | 9.60 | 9.70 | 9.80 | 9.90 |
人数 | 2 | 3 | 5 | 4 | 3 | 1 |
则入围同学决赛成绩的中位数和众数分别是( )
A. 9.70,9.60 B. 9.60,9.60 C. 9.60,9.70 D. 9.65,9.60
B 【解析】根据中位数和众数的概念求解. ∵共有18名同学, 则中位数为第9名和第10名同学成绩的平均分,即中位数为:=9.60, 众数为:9.60. 故选B.查看答案和解析>>
科目:初中数学 来源:人教版七年级下册数学第7-10章综合测试卷 题型:填空题
生物学研究表明在8﹣17岁期间,男女生身高增长速度规律呈现如图所示,请你观察此图,回答下列问题:男生身高增长速度的巅峰期是________ 岁,在________ 岁时男生女生的身高增长速度是一样的.
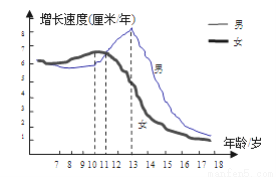
查看答案和解析>>
科目:初中数学 来源:北师大版数学九年级下册 1.1 锐角三角函数 题型:解答题
如图所示,在Rt△ACB中,∠C=90°,AB=3,BC=1,求∠A的三角函数值.
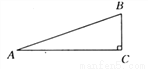
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com