
(2015秋•重庆校级期中)感恩节即将来临,小王调查了初三年级部分同学在感恩节当天将以何种方式对帮助过自己的人表达感谢,他将调查结果分为如下四类:A类﹣﹣当面表示感谢、B类﹣﹣打电话表示感谢、C类﹣﹣发短信表示感谢、D类﹣﹣写书信表示感谢.他将调查结果绘制成了如图所示的扇形统计图和条形统计图.请你根据图中提供的信息完成下列各题:
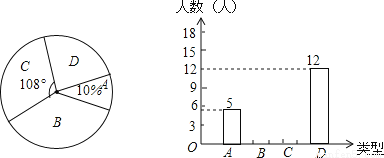
(1)补全条形统计图;
(2)在A类的同学中,有4人来自同一班级,其中有2人主持过班会.现准备从他们4人中随机抽出两位同学主持感恩节主题班会课,请用树状图或列表法求抽出1人主持过班会而另一人没主持过班会的概率.
(1)见解析;(2) 【解析】 试题分析:(1)观察统计图,先用A类的人数除以它所占的百分比得到总人数,再利用扇形统计图计算出C类人数,接着计算出D类人数,然后补全条形统计图; (2)通过列表法展示所有12种等可能情况,再找出1人主持过班会而另一人没主持过班会的结果数,然后根据概率公式求解. 【解析】 (1)调查的学生总数为5÷10%=50(人), C类人数为50×...科目:初中数学 来源:2017年广东省佛山市中考数学模拟试卷(3) 题型:单选题
2003年6月1日,举世瞩目的三峡工程正式下闸蓄水,26台机组发电量将达到84700000000千瓦时,用科学记数法表示为( )
A. 8.47×1010千瓦时 B. 8.47×108千瓦时
C. 8.47×109千瓦时 D. 8.47×1011千瓦时
A 【解析】84 700 000 000=8.47×1010千瓦时. 故选A.查看答案和解析>>
科目:初中数学 来源:2017-2018学年江苏省苏州市初三上期中模拟数学试卷 题型:解答题
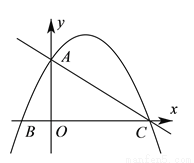
如图,抛物线与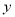 轴交于点
轴交于点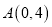 ,与
,与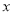 轴交于
轴交于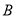 、
、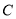 两点,其中
两点,其中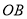 、
、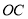 是方程的
是方程的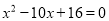 两根,且
两根,且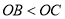 .
.
(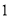 )求抛物线的解析式;
)求抛物线的解析式;
( )直线
)直线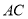 上是否存在点
上是否存在点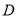 ,使
,使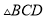 为直角三角形.若存在,求所有
为直角三角形.若存在,求所有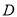 点坐标;反之说理;
点坐标;反之说理;
(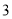 )点
)点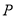 为
为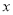 轴上方的抛物线上的一个动点(
轴上方的抛物线上的一个动点(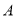 点除外),连
点除外),连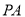 、
、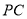 ,若设
,若设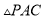 的面积为
的面积为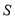 .
. 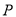 点横坐标为
点横坐标为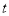 ,则
,则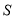 在何范围内时,相应的点
在何范围内时,相应的点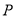 有且只有
有且只有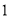 个.
个.
查看答案和解析>>
科目:初中数学 来源:2017-2018学年江苏省苏州市初三上期中模拟数学试卷 题型:单选题
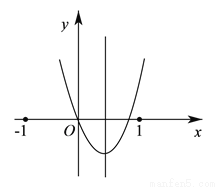
二次函数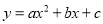 的图象如图所示,那么
的图象如图所示,那么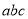 ,
, 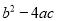 ,
, 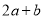 ,
, 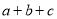 这四个代数式中,值为正数的有( ).
这四个代数式中,值为正数的有( ).
A. 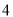 个 B.
个 B. 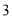 个 C.
个 C. 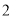 个 D.
个 D. 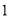 个
个
查看答案和解析>>
科目:初中数学 来源:2017-2018学年江苏省苏州市初三上期中模拟数学试卷 题型:单选题
下列方程为一元二次方程的是( ).
A. 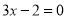 B.
B. 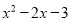 C.
C. 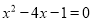 D.
D. 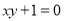
查看答案和解析>>
科目:初中数学 来源:2017年天津市中考数学模拟试卷 题型:填空题
有一枚材质均匀的正方体骰子,它的六个面上分别有1点、2点、…6点的标记,掷一次骰子,向上的一面出现的点数是3的倍数的概率是 .
. 【解析】 试题分析:共有6种等可能的结果数,其中点数是3的倍数有3和6,从而利用概率公式可求出向上的一面出现的点数是3的倍数的概率:.查看答案和解析>>
科目:初中数学 来源:2017年天津市中考数学模拟试卷 题型:单选题
已知x1,x2是关于x的方程x2+ax﹣2b=0的两实数根,且x1+x2=﹣2,x1•x2=1,则ba的值是( )
A.  B. ﹣
B. ﹣ C. 4 D. ﹣1
C. 4 D. ﹣1
查看答案和解析>>
科目:初中数学 来源:2017年四川省数学九年级(上)期末数学试卷 题型:填空题
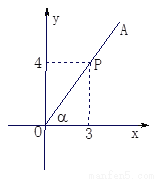
如图,P是∠α的边OA上一点,且点P的坐标为(3,4),则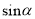 =____________.
=____________.
查看答案和解析>>
科目:初中数学 来源:2017年安徽省中考数学模拟试卷 题型:解答题
在平面直角坐标系中,二次函数y=x2+mx+2m﹣7的图象经过点(1,0).
(1)求抛物线的表达式;
(2)把﹣4<x<1时的函数图象记为H,求此时函数y的取值范围;
(3)在(2)的条件下,将图象H在x轴下方的部分沿x轴翻折,图象H的其余部分保持不变,得到一个新图象M.若直线y=x+b与图象M有三个公共点,求b的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com