
某商店6月份的利润是4800元,8月份的利润达到6500元.设平均每月利润增长的百分率为x,可列方程为( )
A. 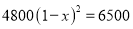 B.
B. 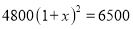
C. 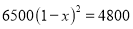 D.
D. 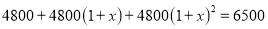
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:人教版2017-2018学年九年级下册数学全册综合测试卷 题型:解答题
如图,已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(﹣1,0),对称轴为直线x=1,与y轴的交点B在(0,2)和(0,3)之间(包括这两点),下列结论:
①当x>3时,y<0; ②3a+b<0; ③﹣1≤a≤﹣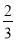 ; ④4ac﹣b2>8a;其中正确的结论是( )
; ④4ac﹣b2>8a;其中正确的结论是( )
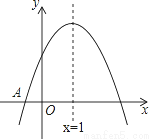
A. ①③④ B. ①②③ C. ①②④ D. ①②③④
B 【解析】试题分析:①由抛物线的对称性可求得抛物线与x轴令一个交点的坐标为(3,0),当x>3时,y<0,故①正确; ②抛物线开口向下,故a<0,∵x=﹣=1,∴2a+b=0.∴3a+b=0+a=a<0,故②正确; ③设抛物线的解析式为y=a(x+1)(x﹣3),则y=ax2﹣2ax﹣3a,令x=0得:y=﹣3a. ∵抛物线与y轴的交点B在(0,2)和(0,3)之间,∴2...查看答案和解析>>
科目:初中数学 来源:2017-2018学年九年级数学北师大版上册 全册综合测试卷1 题型:单选题
如图是一个三棱柱笔筒,则该物体的主视图是( )
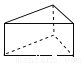
A. 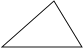 B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源:江苏省张家港市2017-2018学年第一学期初三数学期末考试试卷 题型:填空题
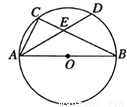
如图, 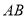 为⊙
为⊙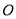 的直径,
的直径, 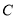 为⊙
为⊙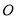 上一点,弦
上一点,弦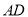 平分
平分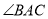 ,交
,交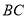 于点
于点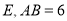 ,
, 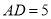 ,则
,则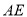 的长为________.
的长为________.
查看答案和解析>>
科目:初中数学 来源:江苏省张家港市2017-2018学年第一学期初三数学期末考试试卷 题型:填空题
已知tanA=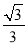 ,则锐角A的度数是__________.
,则锐角A的度数是__________.
查看答案和解析>>
科目:初中数学 来源:江苏省张家港市2017-2018学年第一学期初三数学期末考试试卷 题型:单选题
方程x(x﹣2)=0的解是( )
A. x=0 B. x=2 C. x=0或x=﹣2 D. x=0或x=2
D 【解析】试题分析:原方程已化为了方程左边为两个一次因式的乘积,方程的右边为0的形式;可令每一个一次因式为零,得到两个一元一次方程,从而求出原方程的解. 【解析】 由题意,得:x=0或x﹣2=0, 解得x=0或x=2;故选D.查看答案和解析>>
科目:初中数学 来源:2018人教版九年级数学下册练习:期中检测卷 题型:解答题
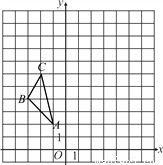
如图,在平面直角坐标系中,已知△ABC三个顶点的坐标分别为A(-1,2),B(-3,4),C(-2,6).
(1)画出△ABC绕点A顺时针旋转90°后得到的△A1B1C1;
(2)以原点O为位似中心,画出将△A1B1C1三条边放大为原来的2倍后的△A2B2C2.
查看答案和解析>>
科目:初中数学 来源:2018人教版九年级数学下册练习:期中检测卷 题型:单选题
已知△ABC∽△A′B′C′且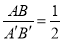 ,则S△ABC∶S△A′B′C′为( )
,则S△ABC∶S△A′B′C′为( )
A. 1∶2 B. 2∶1 C. 1∶4 D. 4∶1
C 【解析】试题解析:∵△ABC∽△A′B′C′,, ∴, 故选C.查看答案和解析>>
科目:初中数学 来源:2017-2018学年八年级数学北师大版上册 全册综合测试卷 题型:解答题
正方形OABC的边长为2,其中OA、OC分别在x轴和y轴上,如图①所示,直线l经过A、C两点.
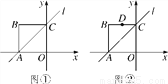
(1)若点P是直线l上的一点,当△OPA的面积是3时,请求出点P的坐标;
(2)如图②,坐标系xOy内有一点D(-1,2),点E是直线l上的一个动点.
①请求出|BE+DE|的最小值和此时点E的坐标;
②若将点D沿x轴翻折到x轴下方,直接写出|BE-DE|的最大值,并写出此时点E的坐标.
(1)P(1,3)或P (-5,-3);(2)①最小值为 ,E ;②最大值为,点E (2,4). 【解析】(1)如图1中,求出直线l的解析式为y=x+2.设点P的坐标为(m,m+2),由题意得×2×|m+2|=3,解方程即可; (2)如图2中,连接OD交直线l于点E,则点E为所求,此时|BE+DE|=|OE+DE|=OD,OD即为最大值.求出直线OD的解析式,利用方程组求出等E坐标即可...查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com