
已知线段AB=20cm,点C为线段AB上一点,且BC=6cm, M是线段AC的中点,则线段AM的长度为_____cm.
7 【解析】试题解析:如图所示: M是线段AC的中点, 故答案为:7.科目:初中数学 来源:山东省泰安市宁阳县2017-2018学年九年级上学期期末质量检测数学试卷 题型:单选题
如图所示,抛物线y=ax2+bx+c的顶点为B(–1,3),与x轴的交点A在点(–3,0)和(–2,0)之间,以下结论:①b2–4ac=0;②a+b+c>0;③2a–b=0;④c–a=3.其中正确的有( )
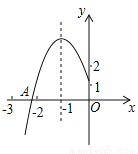
A. 1个 B. 2个 C. 3个 D. 4个
B 【解析】试题分析:根据图像可得:二次函数与x轴有两个交点,则,故①错误;根据函数的对称性可知:当x=1时,y0,即a+b+c0,故②错误;根据题意可知:函数的对称轴为直线x=-1,即,则2a-b=0,则③正确;当x=-1时,y=3,则a-b+c=3,根据③可知b=2a,则a-b+c=a-2a+c=c-a=3,故④正确;故本题选B.查看答案和解析>>
科目:初中数学 来源:江苏省扬州市邗江区2017-2018学年八年级上学期期末考试数学试卷 题型:填空题
若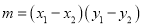 ,且A
,且A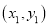 、B
、B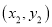 是一次函数
是一次函数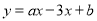 图像上两个不同的点,当
图像上两个不同的点,当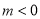 时,a的取值范围是______.
时,a的取值范围是______.
查看答案和解析>>
科目:初中数学 来源:江苏省扬州市邗江区2017-2018学年八年级上学期期末考试数学试卷 题型:单选题
下面四个图案中,不是轴对称图形的是( )
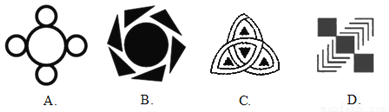
A. A B. B C. C D. D
B 【解析】A是轴对称图形,不符合题意;B不是轴对称图形,符合题意;C是轴对称图形,不符合题意;D是轴对称图形,不符合题意, 故选B.查看答案和解析>>
科目:初中数学 来源:江苏省无锡市2017-2018学年七年级上学期期末考试数学试卷 题型:解答题
解方程:
(1)3x+4-5(x+1)=-1; (2)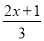 -
-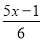 =1.
=1.
查看答案和解析>>
科目:初中数学 来源:江苏省无锡市2017-2018学年七年级上学期期末考试数学试卷 题型:单选题
如图,∠ABC=∠ACB,AD、BD、CD分别平分△ABC的外角∠EAC、内角∠ABC、外角∠ACF.以下结论:① AD∥BC;② ∠ACB=2∠ADB;③ ∠ADC=90°-∠ABD;④ BD平分∠ADC;⑤ 2∠BDC=∠BAC.其中正确的结论有 ( )
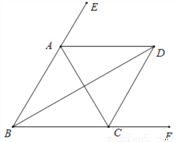
A. ①②④ B. ①③④⑤ C. ①②③⑤ D. ①②③④⑤
C 【解析】试题解析:(1)∵AD平分△ABC的外角∠EAC, ∴∠EAD=∠DAC, ∵∠EAC=∠ACB+∠ABC,且∠ABC=∠ACB, ∴∠EAD=∠ABC, ∴ADBC, 故①正确. (2)由(1)可知ADBC, ∴∠ADB=∠DBC, ∵BD平分∠ABC, ∴∠ABD=∠DBC, ∴∠ABC=2∠ADB, ∵∠AB...查看答案和解析>>
科目:初中数学 来源:江苏省无锡市2017-2018学年七年级上学期期末考试数学试卷 题型:单选题
下列计算正确的是( )
A. 3a+4b=7ab B. 7a﹣3a=4 C. 3ab﹣2ab=ab D. 3a+2a=5a2
C 【解析】试题分析:根据合并同类项法则:只把系数相加,先确定同类项,然后再合并即可. 由此可知3a与4b不是同类项,不能计算,故A不正确; 7a-3a=4a,故B不正确; 3ab-2ab=ab,故C正确; 3a+2a=5a,故D不正确. 故选:C查看答案和解析>>
科目:初中数学 来源:湖北省襄阳市襄城区2017-2018学年七年级上学期期末考试数学试卷 题型:单选题
成都市为减少雾霾天气采取了多项措施,如对城区主干道进行绿化.现计划把某一段公路的一侧全部栽上银杏树,要求路的两端各栽一棵,并且每两棵树的间隔相等.如果每隔5米栽1棵,则树苗缺21棵;如果每隔6米栽1棵,则树苗正好用完.设原有树苗x棵,则根据题意列出方程正确的是( )
A. 5(x+21﹣1)=6(x﹣l) B. 5(x+21)=6(x﹣l) C. 5(x+21﹣1)=6x D. 5(x+21)=6x
A 【解析】【解析】 因为设原有树苗x棵,则路的长度为5(x+21﹣1)米,由题意,得 5(x+21﹣1)=6(x﹣1), 故选:A.查看答案和解析>>
科目:初中数学 来源:2017-2018年福建厦门市八年级上册数学期末质量检测试卷 题型:解答题
如图,已知点B,C,E,F在同一直线上,AB=DE,BE=CF,∠B=∠DEF,求证:∠ACE=∠D+∠DEF.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com