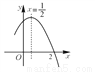
如图.二次函数y=ax2+bx+c图象的一部分.对称轴为直线x= .且经过点(2.0).下列说法:①abc<0,②a+b=0,③4a+2b+c<0,④若.(.y2)是抛物线上的两点.则y1＜y2.其中说法正确的是( ) A. ①②④ B. ③④ C. ①③④ D. ①② A [解析][解析] ①∵二次函数的图象开口向下.∴a＜0.∵二次函数的图象交y轴的正半轴题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

如图，二次函数y=ax2+bx+c(a≠0)图象的一部分，对称轴为直线x=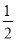 ，且经过点(2，0).下列说法：①abc<0；②a+b=0；③4a+2b+c<0；④若(-2，y1)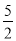，(，y2)是抛物线上的两点，则y1＜y2，其中说法正确的是( )

A. ①②④ B. ③④ C. ①③④ D. ①②

A 【解析】【解析】 ①∵二次函数的图象开口向下，∴a＜0，∵二次函数的图象交y轴的正半轴于一点，∴c＞0，∵对称轴是直线x=，∴ =，∴b=﹣a＞0，∴abc＜0．故①正确； ②∵由①中知b=﹣a，∴a+b=0，故②正确； ③把x=2代入y=ax2+bx+c得：y=4a+2b+c，∵抛物线经过点（2，0），∴当x=2时，y=0，即4a+2b+c=0．故③错误；...

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源：北师大版七年级上册第五章一元一次方程 5．1　认识一元一次方程同步测试卷含答案 题型：单选题

下列方程的解正确的是（）

A. x－3=1的解是x=－2 B. 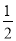x－2x=6的解是x=－4

C. 3x－4=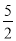（x－3）的解是x=3 D. 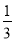－x=2的解是x=－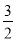

B 【解析】本题考查的是一元一次方程的解的定义.方程的解就是能够使方程两边左右相等的未知数的值，即利用方程的解代替未知数，所得到的式子左右两边相等． A.把x=-2代入x-3=1，左边=-2-3=-5，左边≠右边，因而x=-2不是方程x-3=1的解． B.把x=-4代入x-2x=6，左边=-2+8=6，左边=右边，因而x-2x=6的解是x=-4． C，把x=3代入3x-4=...

查看答案和解析>>

科目：初中数学 来源：人教版数学七年级下册（贵州专版）期中综合检测 题型：解答题

如图所示,直线AB,CD,EF相交于点O,∠DOB的度数是它余角的2,∠AOE=2∠DOF,OG⊥AB.

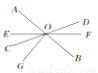
求：(1)∠DOB的度数;

(2)∠BOF的度数;

(3)∠EOG的度数.

(1)∠DOB=60°;(2)∠BOF =40°; (3)∠EOG=50°. 【解析】试题分析: （1）首先根据垂直定义可得∠GOB=90°，根据平角定义可得∠COG+∠DOB=90°，再根据∠DOB是它余角的2倍可得∠DOB+∠DOB=90°，进而可算出∠DOB的度数；（2）首先根据对顶角相等可得∠AOC的度数，再根据∠AOE=2∠DOF可得3∠COE=60°，继而可得∠COE=2...

查看答案和解析>>

科目：初中数学 来源：人教版数学七年级下册（贵州专版）期中综合检测 题型：单选题

点P是直线l外一点,点A,B,C是直线l上三点,且PA=10,PB=8,PC=6,那么点P到直线l的距离为(　　)

A. 6 B. 8 C. 小于6的数 D. 不大于6的数

D 【解析】在PA,PB,PC中PC最小, 若PC垂直l,则PC是垂线段, P到l的距离就是PC=6, 若PC不垂直l, 则PC大于垂线段的长度, P到l的距离小于PC=6. 故选D.

查看答案和解析>>

科目：初中数学 来源：人教版九年级上册数学 22.2二次函数与一元二次方程练习 题型：单选题

如图，二次函数y=ax2+bx+c（a≠0）的图象与x轴正半轴相交于A、B两点，与y轴相交于点C，对称轴为直线x=2，且OA=OC，则下列结论：①abc＞0；②9a+3b+c＜0；③c＞﹣1；④关于x的方程ax2+bx+c=0（a≠0）有一个根为 -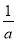，其中正确的结论个数有_____________________ （填序号）

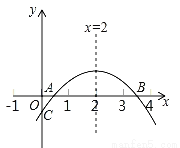
C 【解析】试题分析:由图象可知抛物线开口向下，可得a＜0，由抛物线的对称轴在y轴的右侧，可得b＞0，抛物线与y轴的交点在x轴下方，可得c＜0，所以abc＞0，即①正确；当x=3时，y=ax2+bx+c=9a+3b+c＞0，所以②错误；已知C（0，c），OA=OC，可得A（﹣c，0），由图知，A在1的左边 ∴﹣c＜1 ，即c＞－1，即③正确；把－代入方程ax2+bx+c="0" (a≠...

查看答案和解析>>

科目：初中数学 来源：人教版九年级上册数学 22.2二次函数与一元二次方程练习 题型：单选题

二次函数y=ax2+bx+c（a≠0）的图象如图所示，则下列结论中正确的是（　　）

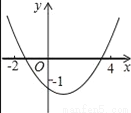
A. c＞﹣1 B. b＞0 C. 2a+b≠0 D. 9a+c＞3b

D 【解析】由抛物线与y轴的交点在点（0，﹣1）的下方得到c＜﹣1；由抛物线开口方向得a＞0，再由抛物线的对称轴在y轴的右侧得a、b异号，即b＜0；根据抛物线的对称性得到抛物线对称轴为直线x=﹣，若x=1，则2a+b=0，故可能成立；由于当x=﹣3时，y＞0，所以9a﹣3b+c＞0，即9a+c＞3b．【解析】 ∵抛物线与y轴的交点在点（0，﹣1）的下方． ∴c＜﹣1； ...

查看答案和解析>>

科目：初中数学 来源：初一数学第一学期4.3角同步练习 题型：填空题

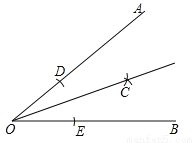
如图所示，已知∠AOB=40°，现按照以下步骤作图：

①在OA，OB上分别截取线段OD，OE，使OD=OE；

②分别以D，E为圆心，以大于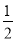DE的长为半径画弧，在∠AOB内两弧交于点C；