
科目: 来源:江苏省2017-2018学年上期八年级9月月考数学试卷 题型:填空题
如图 ,已知
,已知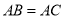 ,
, 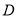 为
为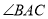 的角平分线上面一点,连接
的角平分线上面一点,连接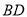 、
、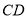 ;如图
;如图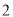 ,已知
,已知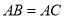 ,
, 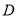 、
、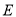 为
为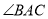 的角平分线上面两点,连接
的角平分线上面两点,连接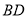 、
、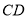 、
、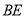 、
、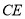 ;如图
;如图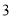 ,已知
,已知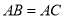 ,
, 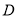 、
、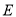 、
、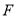 为
为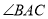 的角平分线上面三点,连接
的角平分线上面三点,连接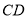 、
、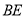 、
、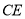 、
、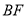 、
、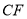 ;…,依次规律,第
;…,依次规律,第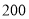 个图形中全等三角形的对数是 _______.
个图形中全等三角形的对数是 _______.

查看答案和解析>>
科目: 来源:江苏省2017-2018学年上期八年级9月月考数学试卷 题型:填空题
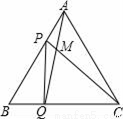
如图,点P、Q分别是边长为4cm的等边△ABC边AB、BC上的动点,点P从顶点A,点Q从顶点B同时出发,且它们的速度都为1cm/s,下面四个结论正确的有________________.
①BP=CM;②△ABQ≌△CAP;③∠CMQ的度数不变,始终等于60°;④当第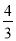 秒或第
秒或第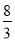 秒时,△PBQ为直角三角形.
秒时,△PBQ为直角三角形.
查看答案和解析>>
科目: 来源:江苏省2017-2018学年上期八年级9月月考数学试卷 题型:解答题
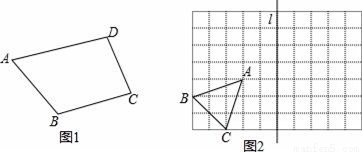
(1)尺规作图:如图1,在四边形ABCD内找一点P,使得点P到AB、BC的距离相等,并且点P到点A、D的距离也相等.(不写作法,保留作图痕迹).
(2)如图2,在长度为1个单位长度的小正方形组成的正方形网格中,点A、B、C在小正方形的顶点上,①△ABC的面积为______.
②在图中画出与△ABC关于直线l成轴对称的△A1B1C1.
查看答案和解析>>
科目: 来源:江苏省2017-2018学年上期八年级9月月考数学试卷 题型:解答题
如图,△ABC中,边AB、AC的垂直平分线分别交BC于D、E.
(1)若BC=10,则△ADE周长是多少?为什么?
(2)若∠BAC=128°,则∠DAE的度数是多少?为什么?

查看答案和解析>>
科目: 来源:江苏省2017-2018学年上期八年级9月月考数学试卷 题型:解答题
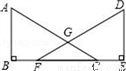
如图,点B、F、C、E存同一直线上,AC、DF相交于点G,AB⊥BE,垂足为B,DE⊥BE,垂足为E,且AC=DF,BF=CE.
(1)求证:△ABC≌△DEF;
(2)若∠A=65°,求∠AGF的度数
查看答案和解析>>
科目: 来源:江苏省2017-2018学年上期八年级9月月考数学试卷 题型:解答题
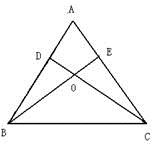
已知:如图,锐角△ABC的两条高BE、CD相交于点O,且OB=OC,
(1)求证:△ABC是等腰三角形;
(2)判断点O是否在∠BAC的角平分线上,并说明理由。
查看答案和解析>>
科目: 来源:江苏省2017-2018学年上期八年级9月月考数学试卷 题型:解答题
我校快乐走班数学兴趣小组开展了一次活动,过程如下:设∠BAC=θ(0°<θ<90°)小棒依次摆放在两射线之间,并使小棒两端分别落在两射线上.
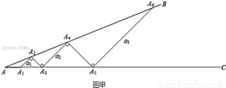
活动一:如图甲所示,从点A1开始,依次向右摆放小棒,使小棒与小棒在端点处互相垂直,A1A2为第1根小棒.
数学思考:
(1)小棒能无限摆下去吗?答: .(填“能“或“不能”)
(2)设AA1=A1A2=A2A3=1.则θ= 度;
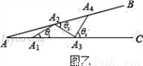
活动二:如图乙所示,从点A1开始,用等长的小棒依次向右摆放,其中A1A2为第1根小棒,且A1A2=AA1.
数学思考:
(3)若只能摆放5根小棒,求θ的范围.
查看答案和解析>>
科目: 来源:江苏省2017-2018学年上期八年级9月月考数学试卷 题型:解答题
如图1,在正方形ABCD中,M是BC边(不含端点B、C)上任意一点,P是BC延长线上一点,N是∠DCP的平分线上一点.若∠AMN=90°,求证:AM=MN.
下面给出一种证明的思路,你可以按这一思路证明,也可以选择另外的方法证明.
证明:在边AB上截取AE=MC,连ME.
正方形ABCD中,∠B=∠BCD=90°,AB=BC.
∴∠NMC=180°—∠AMN—∠AMB
=180°—∠B—∠AMB
=∠MAB=∠MAE.
(下面请你完成余下的证明过程)
(2)若将(1)中的“正方形ABCD”改为“正三角形ABC”(如图2),N是∠ACP的平分线上一点,则当∠AMN=60°时,结论AM=MN是否还成立?请说明理由.
(3)若将(1)中的“正方形ABCD”改为“正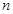 边形ABCD…X”,请你作出猜想:当∠AMN= °时,结论AM=MN仍然成立.(直接写出答案,不需要证明)
边形ABCD…X”,请你作出猜想:当∠AMN= °时,结论AM=MN仍然成立.(直接写出答案,不需要证明)
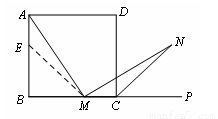
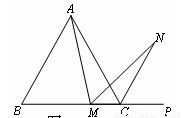
图1 图2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com