
科目: 来源:2017年秋(北师大版)九年级数学下册(河南)检测:2.2 二次函数的图象与性质 题型:单选题
已知二次函数y=2(x﹣3)2+1,下列说法:
①其图象的开口向下;
②其图象的对称轴为直线x=﹣3;
③其图象顶点坐标为(3,﹣1);
④当x<3时,y的值随x值的增大而减小.
则其中说法正确的有( )
A. 1个 B. 2个 C. 3个 D. 4个
A 【解析】试题分析:结合二次函数解析式,根据函数的性质对各小题分析判断解答即可. 【解析】 ①∵2>0,∴图象的开口向上,故①正确; ②图象的对称轴为直线x=3,故②正确; ③其图象顶点坐标为(3,1),故③正确; ④当x<3时,y随x的增大而减小,正确; 综上所述,说法正确4个. 故选D.查看答案和解析>>
科目: 来源:2017年秋(北师大版)九年级数学下册(河南)检测:2.2 二次函数的图象与性质 题型:填空题
把抛物线y=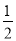 (x-1)2+2向左平移1个单位长度,再向下平移2个单位长度,则所得抛物线的表达式为________.
(x-1)2+2向左平移1个单位长度,再向下平移2个单位长度,则所得抛物线的表达式为________.
查看答案和解析>>
科目: 来源:2017年秋(北师大版)九年级数学下册(河南)检测:2.2 二次函数的图象与性质 题型:填空题
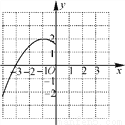
如图是二次函数y=a(x+1)2+2图象的一部分,该图象在y轴右侧与x轴交点的坐标是________.
(1,0) 【解析】试题分析:根据函数表达式和函数图像可以看出二次函数的对称轴是x=-1,该图象在y轴左侧与x轴交点的坐标是(-3,0),所以该图象在y轴右侧与x轴交点的坐标与(-3,0) 关于对称轴对称,所以该图象在y轴右侧与x轴交点的坐标是(1,0)查看答案和解析>>
科目: 来源:2017年秋(北师大版)九年级数学下册(河南)检测:2.2 二次函数的图象与性质 题型:单选题
若抛物线y=(x-m)2+(m+1)的顶点在第一象限,则m的取值范围为( )
A. m>1 B. m>0 C. m>-1 D. -1<m<0
B 【解析】试题分析:利用y=ax2+bx+c的顶点坐标公式表示出其顶点坐标,根据顶点在第一象限,所以顶点的横坐标和纵坐标都大于0列出不等式组.查看答案和解析>>
科目: 来源:2017年秋(北师大版)九年级数学下册(河南)检测:2.2 二次函数的图象与性质 题型:单选题
已知二次函数y=a(x-1)2-c的图象如图所示,则一次函数y=ax+c的大致图象可能是( )
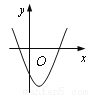
A. 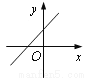 B.
B. 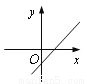 C.
C. 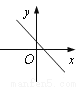 D.
D. 
查看答案和解析>>
科目: 来源:2017年秋(北师大版)九年级数学下册(河南)检测:2.2 二次函数的图象与性质 题型:单选题
已知二次函数y=(x﹣h)2+1(h为常数),在自变量x的值满足1≤x≤3的情况下,与其对应的函数y的最小值为5,则h的值是( )
A. ﹣1 B. ﹣1或5 C. 5 D. ﹣5
B 【解析】∵当x>h时,y随x的增大而增大,当x<h时,y随x的增大而减小, ∴①若h<1≤x≤3,x=1时,y取得最小值5, 可得:(1﹣h)2+1=5, 解得:h=﹣1或h=3(舍); ②若1≤x≤3<h,当x=3时,y取得最小值5, 可得:(3﹣h)2+1=5, 解得:h=5或h=1(舍). 综上,h的值为﹣1或5, 故选B. ...查看答案和解析>>
科目: 来源:2017年秋(北师大版)九年级数学下册(河南)检测:2.2 二次函数的图象与性质 题型:填空题
已知点A(4,y1),B(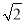 ,y2),C(﹣2,y3)都在二次函数y=(x﹣2)2﹣1的图象上,则y1、y2、y3的大小关系是_____.
,y2),C(﹣2,y3)都在二次函数y=(x﹣2)2﹣1的图象上,则y1、y2、y3的大小关系是_____.
查看答案和解析>>
科目: 来源:2017年秋(北师大版)九年级数学下册(河南)检测:2.2 二次函数的图象与性质 题型:解答题
把二次函数y=a(x-h)2+k的图象先向左平移2个单位,再向上平移4个单位,得到二次函数y=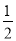 (x+1)2-1的图象.
(x+1)2-1的图象.
(1)试确定a,h,k的值;
(2)指出二次函数y=a(x-h)2+k的开口方向,对称轴和顶点坐标.
(1)a=,h=1,k=-5;(2)开口向上,对称轴为x=1,顶点坐标为(1,-5). 【解析】试题分析:(1)二次函数的平移,可以看作是将二次函数y= (x+1)2-1先向右平移2个单位,再向下平移4个单位得到二次函数y=a(x-h)2+k,然后再按二次函数图象的平移法则,确定函数解析式,即可得到结论; (2),直接根据函数解析式,结合二次函数的性质,进行回答即可. 试题分析:...查看答案和解析>>
科目: 来源:2017年秋(北师大版)九年级数学下册(河南)检测:2.2 二次函数的图象与性质 题型:解答题
已知:抛物线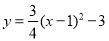 .
.
(1)写出抛物线的开口方向、对称轴;
(2)函数y有最大值还是最小值?并求出这个最大(小)值;
(3)设抛物线与y轴的交点为P,与x轴的交点为Q,求直线PQ的函数解析式.
【解析】 (1)抛物线, ∵a= >0, ∴抛物线的开口向上, 对称轴为x=1; (2)∵a=>0, ∴函数y有最小值,最小值为-3; (3)令x=0,则 , 所以,点P的坐标为(0, ), 令y=0,则, 解得x1=-1,x2=3, 所以,点Q的坐标为(-1,0)或(3,0), 当点P(0, ),Q(-1,0)时,设直线PQ的解析式...查看答案和解析>>
科目: 来源:2017年秋(北师大版)九年级数学下册(河南)检测:2.2 二次函数的图象与性质 题型:解答题
已知:如图,二次函数y=a(x﹣h)2+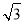 的图象经过原点O(0,0),A(2,0).
的图象经过原点O(0,0),A(2,0).
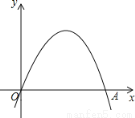
(1)写出该函数图象的对称轴;
(2)若将线段OA绕点O逆时针旋转60°到OA′,试判断点A′是否为该函数图象的顶点?请说明理由.
(1)直线x=1 (2)点A′为抛物线y=﹣(x﹣1)2+的顶点 【解析】 试题分析:(1)把已知点O、A代入函数的解析式可求出h的值h=1,及a=,然后根据二次函数的顶点式的特点判断出对称轴; (2)由线段OA绕点O逆时针旋转60°到OA′,可知OA′=OA=2,∠A′OA=60°,如图,作A′B⊥x轴于点B,根据直角三角形的特点可知sin60°=,cos60°=,因此可求得A...查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com