
科目: 来源:数学人教版八年级上册第11章第二节与三角形有关的角第一课时同步练习 题型:填空题
如图,点B,C,E,F在同一直线上,AB∥DC,DE∥GF,∠B=∠F=72°,则∠D=________.

查看答案和解析>>
科目: 来源:数学人教版八年级上册第11章第二节与三角形有关的角第一课时同步练习 题型:填空题
当三角形中一个内角α是另一个内角β的两倍时,我们称此三角形为“特征三角形”,其中α称为“特征角”.如果一个“特征三角形”的“特征角”为100°,那么这个“特征三角形”的最小内角的度数为________.
30° 【解析】试题分析:此题主要考查了新定义以及三角形的内角和定理,根据已知得出β的度数是解题关键.根据已知一个内角α是另一个内角β的两倍得出β的度数,进而求出最小内角即可. 由题意得:α=2β,α=110°,则β=55°, 180°-110°-55°=15°, 故答案为:15°.查看答案和解析>>
科目: 来源:数学人教版八年级上册第11章第二节与三角形有关的角第一课时同步练习 题型:填空题
小明在学习三角形内角和定理时,自己做了如下推理过程,请你帮他补充完整.
已知:如图,△ABC中,∠A、∠B、∠C是它的三个内角,那么这三个内角的和等于多少?为什么?

【解析】
∠A+∠B+∠C=180°
理由:作∠ACD=∠A,并延长BC到E
∠1=∠A(已作)
∴AB∥CD (_________________________)
∴∠B=_____(_________________________)
而∠ACB+∠1+∠2=180°
∴∠ACB+_____+_____=180°(等量代换)
内错角相等,两直线平行;∠2;两直线平行,同位角相等;∠B;∠A. 【解析】试题分析:作∠ACD=∠A,并延长BC到E.利用平行线的判定推知AB∥CD,然后根据平行线的性质可知∠B=∠2;最后由等量代换证得∠ACB+∠B+∠A=180°. 试题解析:【解析】 ∠A+∠B+∠C=180°. 理由:作∠ACD=∠A,并延长BC到E ∠1=∠A(已作) ∴AB∥CD (内...查看答案和解析>>
科目: 来源:数学人教版八年级上册第11章第二节与三角形有关的角第一课时同步练习 题型:解答题
如图,已知△ABC的AC边的延长线AD∥EF,若∠A=60°,∠B=43°,试用推理的格式求出∠E的大小.
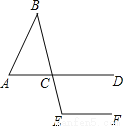
查看答案和解析>>
科目: 来源:数学人教版八年级上册第11章第二节与三角形有关的角第一课时同步练习 题型:解答题
如图1,在△ABC中,OB、OC是∠ABC、∠ACB的角平分线;
(1)填写下面的表格.
∠A的度数 | 50° | 60° | 70° |
∠BOC的度数 |
(2)试猜想∠A与∠BOC之间存在一个怎样的数量关系,并证明你的猜想;
(3)如图2,△ABC的高BE、CD交于O点,试说明图中∠A与∠BOD的关系.
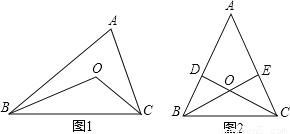
查看答案和解析>>
科目: 来源:数学人教版八年级上册第11章第二节与三角形有关的角第一课时同步练习 题型:解答题
将一副三角板拼成如图所示的图形,过点C作CF平分∠DCE交DE于点F.
(1)求证:CF∥AB;
(2)求∠DFC的度数.

查看答案和解析>>
科目: 来源:数学人教版八年级上册第11章第二节与三角形有关的角第一课时同步练习 题型:解答题
(1).解方程:3x+1=7;
(2).如图,在△ABC中,∠B=35°,∠C=65°,求∠A的度数.
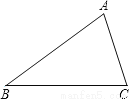
查看答案和解析>>
科目: 来源:陕西省2016-2017学年八年级下学期期末考试数学试卷 题型:单选题
下列美丽的图案,既是轴对称图形又是中心对称图形的个数是( ).




A.  个 B.
个 B.  个 C.
个 C.  个 D.
个 D.  个
个
查看答案和解析>>
科目: 来源:陕西省2016-2017学年八年级下学期期末考试数学试卷 题型:单选题
若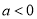 ,则下列不等式不成立的是( ).
,则下列不等式不成立的是( ).
A. 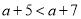 B.
B. 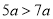 C.
C. 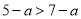 D.
D. 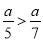
查看答案和解析>>
科目: 来源:陕西省2016-2017学年八年级下学期期末考试数学试卷 题型:单选题
下列因式分解正确的是( ).
A. 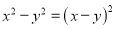 B.
B. 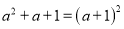 C.
C. 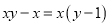 D.
D. 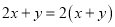
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com