
科目: 来源:贵州省六盘水市2018届九年级上学期第二次月考数学试卷 题型:解答题
已知x1,x2是关于x的一元二次方程x2-2(m+1)x+m2+5=0的两实根.
(1)若(x1-1)(x2-1)=28,求m的值;
(2)已知等腰△ABC的一边长为7,若x1,x2恰好是△ABC另外两边的边长,求这个三角形的周长.
【答案】(1)m的值为6;(2)17.
【解析】试题分析:
(1)由题意和根与系数的关系可得:x1+x2=2(m+1),x1x2=m2+5;由(x1-1)(x2-1)=28,可得:x1x2-(x1+x2)=27;从而得到:m2+5-2(m+1)=27,解方程求得m的值,再由“一元二次方程根的判别式”进行检验即可得到m的值;
(2)①当7为腰长时,则方程的两根中有一根为7,代入方程可解得m的值(此时m的取值需满足根的判别式△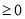 ),将m的值代入原方程,可求得两根(此时两根和7需满足三角形三边之间的关系),从而可求得等腰三角形的周长;
),将m的值代入原方程,可求得两根(此时两根和7需满足三角形三边之间的关系),从而可求得等腰三角形的周长;
②当7为底边时,则方程的两根相等,由此可得“根的判别式△=0”,从而可得关于m的方程,解方程求得m的值,代入原方程可求得方程的两根,再由三角形三边之间的关系检验即可.
试题解析:
(1)(x1-1)(x2-1)=28,即x1x2-(x1+x2)=27,而x1+x2=2(m+1),x1x2=m2+5,
∴m2+5-2(m+1)=27,
解得m1=6,m2=-4,
又Δ=[-2(m+1)]2-4×1×(m2+5)≥0时,m≥2,
∴m的值为6;
(2) 若7为腰长,则方程x2-2(m+1)x+m2+5=0的一根为7,
即72-2×7×(m+1)+m2+5=0,
解得m1=10,m2=4,
当m=10时,方程x2-22x+105=0,根为x1=15,x2=7,不符合题意,舍去.
当m=4时,方程为x2-10x+21=0,根为x1=3,x2=7,此时周长为7+7+3=17
若7为底边,则方程x2-2(m+1)x+m2+5=0有两等根,
∴Δ=0,解得m=2,此时方程为x2-6x+9=0,根为x1=3,x2=3,3+3<7,不成立,
综上所述,三角形周长为17
点睛:(1)一元二次方程根与系数的关系成立的前提条件是方程要有实数根,即“根的判别式△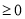 ”;(2)涉及三角形边长的问题中,解得的结果都需要用“三角形三边之间的关系”检验,看三条线段能否围成三角形.
”;(2)涉及三角形边长的问题中,解得的结果都需要用“三角形三边之间的关系”检验,看三条线段能否围成三角形.
【题型】解答题
【结束】
21
如图,已知在△ABC中,D是AB的中点,且∠ACD=∠B,若 AB=10,求AC的长.
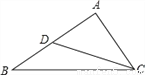
查看答案和解析>>
科目: 来源:贵州省六盘水市2018届九年级上学期第二次月考数学试卷 题型:解答题
如图,已知在△ABC中,D是AB的中点,且∠ACD=∠B,若 AB=10,求AC的长.
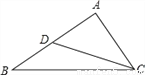
【答案】5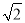 .
.
【解析】试题分析:
由点D是AB的中点,AB=10,易得AD=5;再由∠ACD=∠B,∠A=∠A,可证得:
△ACD∽△ABC,从而可得: 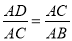 ,由此得到:AC2=AD
,由此得到:AC2=AD AB=50即可解得AC的值.
AB=50即可解得AC的值.
试题解析:
∵∠ACD=∠B,∠A=∠A,
∴△ACD∽△ABC.
∴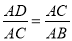 ,
,
∴AC2=AD AB.
AB.
∵D是AB的中点,AB=10,
∴AD=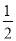 AB=5,
AB=5,
∴AC2=50.
解得AC=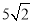 .
.
【题型】解答题
【结束】
22
口袋中装有四个大小完全相同的小球,把它们分别标号1,2,3,4,从中随机摸出一个球,记下数字后放回,再从中随机摸出一个球,利用树状图或者表格求出两次摸到的小球数和等于4的概率.
. 【解析】试题分析: 根据题意列表如下,由表可以得到所有的等可能结果,再求出所有结果中,两次所摸到小球的数字之和为4的次数,即可计算得到所求概率. 试题解析: 列表如下: 1 2 3 4 1 (1,1) (1,2) (1,3) (1,4) 2 (2,1) (2,2) (2,3) ...查看答案和解析>>
科目: 来源:贵州省六盘水市2018届九年级上学期第二次月考数学试卷 题型:解答题
口袋中装有四个大小完全相同的小球,把它们分别标号1,2,3,4,从中随机摸出一个球,记下数字后放回,再从中随机摸出一个球,利用树状图或者表格求出两次摸到的小球数和等于4的概率.
【答案】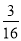 .
.
【解析】试题分析:
根据题意列表如下,由表可以得到所有的等可能结果,再求出所有结果中,两次所摸到小球的数字之和为4的次数,即可计算得到所求概率.
试题解析:
列表如下:
1 | 2 | 3 | 4 | |
1 | (1,1) | (1,2) | (1,3) | (1,4) |
2 | (2,1) | (2,2) | (2,3) | (2,4) |
3 | (3,1) | (3,2) | (3,3) | (3,4) |
4 | (4,1) | (4,2) | (4,3) | (4,4) |
由表可知,共有16种等可能事件,其中两次摸到的小球数字之和等于4的有(3,1)、(2,2)和(1,3),共计3种,
∴P(两次摸到小球的数字之和等于4)=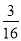 .
.
【题型】解答题
【结束】
23
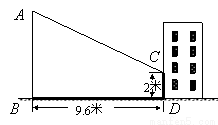
小亮同学想利用影长测量学校旗杆AB的高度,如图,他在某一时刻立1米长的标杆测得其影长为1.2米,同时旗杆的投影一部分在地面上BD处,另一部分在某一建筑的墙上CD处,分别测得其长度为9.6米和2米,求旗杆AB的高度.
查看答案和解析>>
科目: 来源:贵州省六盘水市2018届九年级上学期第二次月考数学试卷 题型:解答题
小亮同学想利用影长测量学校旗杆AB的高度,如图,他在某一时刻立1米长的标杆测得其影长为1.2米,同时旗杆的投影一部分在地面上BD处,另一部分在某一建筑的墙上CD处,分别测得其长度为9.6米和2米,求旗杆AB的高度.
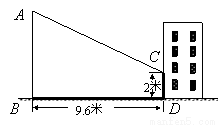
【答案】作DE⊥AB于点E,
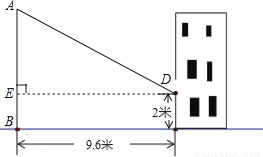
根据题意得: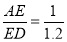 ,
,
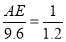 ,
,
解得:AE=8米.
则AB=AE+BE=8+2=10米.
即旗杆的高度为10米.
【解析】根据同一时刻物高与影长成正比,因而作DE⊥AB于点E,则AE与DE的比值,即同一时刻物高与影长的比值,即可求解.
【题型】解答题
【结束】
24
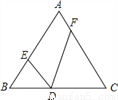
如图,在等边△ABC中,边长为6,D是BC边上的动点,∠EDF=60°.
(1)求证:△BDE∽△CFD;
(2)当BD=1,CF=3时,求BE的长.
查看答案和解析>>
科目: 来源:贵州省六盘水市2018届九年级上学期第二次月考数学试卷 题型:解答题
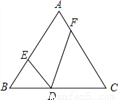
如图,在等边△ABC中,边长为6,D是BC边上的动点,∠EDF=60°.
(1)求证:△BDE∽△CFD;
(2)当BD=1,CF=3时,求BE的长.
【答案】(1)证明见解析;(2) 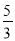
【解析】试题分析:
(1)由题意可得,∠B=∠C=60°,∠BDE+∠CDF=120°,∠BDE+∠BED=120°,由此可得:∠CDF=∠BED,从而可得:△BDE∽△CFD;
(2)由△BDE∽△CFD可得: 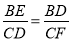 ,由已知易得:CD=BC-BD=5-1=4,由此可得:
,由已知易得:CD=BC-BD=5-1=4,由此可得: 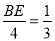 ,解得BE=
,解得BE=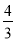 .
.
试题解析:
(1)∵△ABC是等边三角形,
∴∠B=∠C=60°,
∴∠BDE+∠BED=120°.
∵∠EDF=60°,
∴∠BDE+∠CDF=120°,
∴∠CDF=∠BED,
∴△BDE∽△CFD;
(2)∵等边△ABC的边长为5,BD=1,
∴CD=BC-BD=4.
∵△BDE∽△CFD,
∴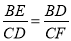 ,即
,即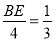 ,
,
∴BE=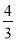 .
.
点睛:本题解题的关键是:由∠EDF=∠B=60°,得到∠BDE+∠BED=120°和∠BDE+∠CDF=120°,从而得到∠BED=∠CDF.
【题型】解答题
【结束】
25
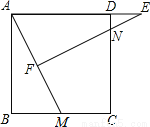
如图,正方形ABCD中,M为BC上一点,F是AM的中点,EF⊥AM,垂足为F,交AD的延长线于点E,交DC于点N.
(1)求证:△ABM ∽△EFA;
(2)若AB=12,BM=5,求DE的长.
查看答案和解析>>
科目: 来源:贵州省六盘水市2018届九年级上学期第二次月考数学试卷 题型:解答题
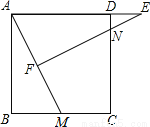
如图,正方形ABCD中,M为BC上一点,F是AM的中点,EF⊥AM,垂足为F,交AD的延长线于点E,交DC于点N.
(1)求证:△ABM ∽△EFA;
(2)若AB=12,BM=5,求DE的长.
【答案】(1)证明见解析;(2)4.9.
【解析】试题分析:(1)由正方形的性质得出AB=AD,∠B=90°,AD∥BC,得出∠AMB=∠EAF,再由∠B=∠AFE,即可得出结论;
(2)由勾股定理求出AM,得出AF,由△ABM∽△EFA得出比例式,求出AE,即可得出DE的长.
试题解析:(1)∵四边形ABCD是正方形,
∴AB=AD,∠B=90°,AD∥BC,
∴∠AMB=∠EAF,
又∵EF⊥AM,
∴∠AFE=90°,
∴∠B=∠AFE,
∴△ABM∽△EFA;
(2)∵∠B=90°,AB=12,BM=5,
∴AM=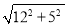 =13,AD=12,
=13,AD=12,
∵F是AM的中点,
∴AF=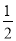 AM=6.5,
AM=6.5,
∵△ABM∽△EFA,
∴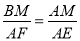 ,
,
即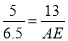 ,
,
∴AE=16.9,
∴DE=AE-AD=4.9.
考点:1.相似三角形的判定与性质;2.正方形的性质.
【题型】解答题
【结束】
26
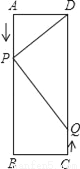
如图,矩形ABCD中,AB=16cm,BC=6cm,点P从点A出发沿AB向点B移动(不与点A、B重合),一直到达点B为止;同时,点Q从点C出发沿CD向点D移动(不与点C、D重合).运动时间设为t秒.
(1)若点P、Q均以3cm/s的速度移动,则:AP= cm;QC= cm.(用含t的代数式表示)
(2)若点P为3cm/s的速度移动,点Q以2cm/s的速度移动,经过多长时间PD=PQ,使△DPQ为等腰三角形?
(3)若点P、Q均以3cm/s的速度移动,经过多长时间,四边形BPDQ为菱形?
查看答案和解析>>
科目: 来源:人教版八年级上册数学第13章13.3《等腰三角形》 题型:单选题
点M(1,2)关于原点对称的点的坐标为 ( )。
A. (—1,2) B. (-1,-2) C. (1,-2) D. (2,-1)
B 【解析】根据关于原点对称的特点,横纵坐标均变为相反数,可得M点的对称点的坐标为(-1,-2). 故选:B.查看答案和解析>>
科目: 来源:人教版八年级上册数学第13章13.3《等腰三角形》 题型:单选题
下列说法正确的是:( )
A.等腰三角形的高、中线、角平分线互相重合
B.顶角相等的两个等腰三角形全等
C.等腰三角形一边不可以是另一边的二倍
D.等腰三角形的两个底角相等
D. 【解析】 试题分析:A.等腰三角形的高、中线、角平分线互相重合,错误; B.顶角相等的两个三角形全等,错误; C.等腰三角形一边不可以是另一边的二倍,错误, D.等腰三角形的两个底角相等,正确; 故选D.查看答案和解析>>
科目: 来源:人教版八年级上册数学第13章13.3《等腰三角形》 题型:单选题
已知∠AOB=30°,点P在∠AOB的内部,点P1与点P关于OB对称,点P2与点P关于OA对称,则以点P1,O,P2为顶点的三角形是( )
A. 直角三角形 B. 钝角三角形 C. 等腰三角形 D. 等边三角形
D 【解析】根据轴对称的性质,进行轴对称变换时对应线段相等,对应角相等, 即, ∠=∠, ∠=∠, 则∠=∠=2(∠BOP+∠POA)=2∠AOB=60°,已知两边相等且一个内角为60°的三角形为等边三角形,故选D.查看答案和解析>>
科目: 来源:人教版八年级上册数学第13章13.3《等腰三角形》 题型:单选题
等腰三角形的对称轴,最多可以有( )
A. 1条 B. 3条 C. 6条 D. 无数条
B 【解析】一般等腰三角形有一条,即底边上的中线所在直线;若是特殊的等腰三角形即等边三角形,则有三条,即每条边上的中线所在直线. 故选:B.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com