
科目: 来源:人教版九年级上册数学 24.2.2直线和圆的位置关系(1)练习 题型:解答题
如图,已知直线AB经过⊙O上的点A,并且AB=OA,?OBA=45?,直线AB是⊙O的切线吗?为什么?

查看答案和解析>>
科目: 来源:人教版九年级上册数学 24.2.2直线和圆的位置关系(1)练习 题型:解答题
如图,直线AB、CD相交于点O,∠AOC=30°,半径为1cm的⊙P的圆心在射线OA上,开始时,PO=6cm,如果⊙P以1cm/秒的速度沿由A向B的方向移动,那么当⊙P的运动时间t(秒)满足什么条件时,⊙P与直线CD相交?
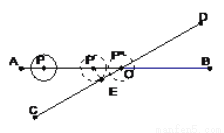
查看答案和解析>>
科目: 来源:人教版九年级上册数学 24.2.2直线和圆的位置关系(1)练习 题型:填空题
如图,以O为圆心的两个同心圆中,大圆的弦AB与小圆相切于点C,若大圆半径为10cm,小圆半径为6cm,则弦AB的长为_______cm.
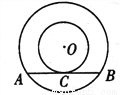
查看答案和解析>>
科目: 来源:人教版九年级上册数学 24.2.2直线和圆的位置关系(1)练习 题型:填空题
如图,直线AB与⊙O相切于点B,BC是⊙O的直径,AC交⊙O于点D,连结BD,则图中直角三角形有______个.
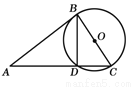
查看答案和解析>>
科目: 来源:人教版九年级上册数学 24.2.2直线和圆的位置关系(1)练习 题型:解答题
如图,线段AB经过圆心O,交⊙O于点A、C,?BAD=?B=30?,边BD交圆于点D.BD是⊙O的切线吗?为什么?
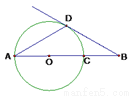
查看答案和解析>>
科目: 来源:人教版九年级上册数学 24.2.2直线和圆的位置关系(1)练习 题型:解答题
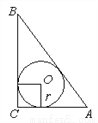
Rt△ABC中,∠C=90°,AC=6,BC=8.求△ABC的内切圆半径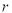 .
.
查看答案和解析>>
科目: 来源:人教版九年级上册数学 24.2.2直线和圆的位置关系(1)练习 题型:解答题
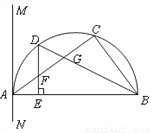
如图,△ABC内接于半圆,AB是直径,过A作直线MN,若∠MAC=∠ABC.
(1)求证:MN是半圆的切线;
(2)设D是弧AC的中点,连结BD交AC 于G,过D作DE⊥AB于E,交AC于F.求证:FD=FG.
查看答案和解析>>
科目: 来源:人教版九年级上册数学 24.2.2直线和圆的位置关系(1)练习 题型:填空题
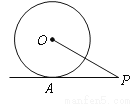
如图,PA是⊙O的切线,切点为A,PA=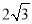 ,∠APO=30°,则
,∠APO=30°,则 的半径长为______.
的半径长为______.
查看答案和解析>>
科目: 来源:人教版九年级上册数学 24.2.2直线和圆的位置关系(1)练习 题型:单选题
如图AB是⊙O的直径,AC是⊙O的切线,A为切点,连结BC交圆0于点D,连结AD,若∠ABC=45 ,则下列结论正确的是( )
,则下列结论正确的是( )
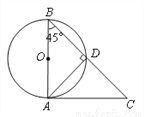
A. AD=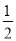 BC B. AD=
BC B. AD=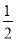 AC C. AC>AB D. AD>DC
AC C. AC>AB D. AD>DC
查看答案和解析>>
科目: 来源:《概率的进一步认识》单元测试2 题型:填空题
抛掷一枚各面分别标有1,2,3,4,5,6的普通骰子,写出这个实验中的一个可能事件: 。
数字6朝上 【解析】 试题分析:根据随机事件的概率结合题意即可得到结果. 答案不唯一,如数字6朝上.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com