
科目: 来源:人教版九年级数学上册经典试卷 第21章 一元二次方程韦达定理 测试卷 题型:填空题
设x1,x2是一元二次方程x2+5x﹣3=0的两根,且2x1(x22+6x2﹣3)+a=4,则a=______.
10 【解析】试题分析:根据一元二次方程的解,由x2是一元二次方程x2+5x﹣3=0的根,代入可得x22+5x2﹣3=0,即x22+5x2=3,然后根据题意2x1(x22+6x2﹣3)+a=4,可得2x1•x2+a=4,再根据一元二次方程根与系数的关系x1+x2=-,x1•x2=,由x1,x2是一元二次方程x2+5x﹣3=0的两根,求得x1x2=﹣3,即2×(﹣3)+a=4,解方程得a=10...查看答案和解析>>
科目: 来源:人教版九年级数学上册经典试卷 第21章 一元二次方程韦达定理 测试卷 题型:填空题
若等腰三角形的一边长为6,另两边长分别是关于x的方程x2﹣(m+2)x+2m+4=0的两个根,则m=__.
6或7 【解析】①当底为6时,m=-2舍去,m=6; ②当腰为6时,m=7. 故答案是:6或7.查看答案和解析>>
科目: 来源:人教版九年级数学上册经典试卷 第21章 一元二次方程韦达定理 测试卷 题型:填空题
关于x的一元二次方程x2-3x+m=0有实数根α、β,且α2+β2=17,则m的值是______.
-4 【解析】一元二次方程x2-3x+m=0有实数根,可得△=b2-4ac=9-4m≥0,解得m≤.根据根与系数的可得 ,所以α2+β2=,解得m=-4.查看答案和解析>>
科目: 来源:人教版九年级数学上册经典试卷 第21章 一元二次方程韦达定理 测试卷 题型:解答题
如果方程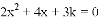 的两个根的平方和等于7,求k的值。
的两个根的平方和等于7,求k的值。
查看答案和解析>>
科目: 来源:人教版九年级数学上册经典试卷 第21章 一元二次方程韦达定理 测试卷 题型:解答题
已知a、b分别是一元二次方程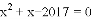 的不相等的两根,求a2+2a+b的值。
的不相等的两根,求a2+2a+b的值。
查看答案和解析>>
科目: 来源:人教版九年级数学上册经典试卷 第21章 一元二次方程韦达定理 测试卷 题型:解答题
关于的一元二次方程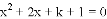 的实数解是
的实数解是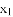 和
和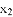 .
.
(1)求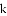
(2)如果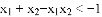 且
且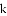
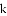
查看答案和解析>>
科目: 来源:人教版九年级数学上册经典试卷 第21章 一元二次方程韦达定理 测试卷 题型:解答题
已知关于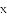
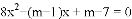 .
.
(1)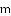
(2)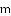
(3)是否存在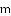
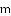
查看答案和解析>>
科目: 来源:人教版九年级数学上册经典试卷 第21章 一元二次方程韦达定理 测试卷 题型:解答题
关于x的一元二次方程x2﹣(m﹣3)x﹣m2=0.
(1)证明:方程总有两个不相等的实数根;
(2)设这个方程的两个实数根为x1,x2,且|x1|=|x2|﹣2,求m的值及方程的根.
(1)证明见解析;(2)x1=﹣1+,x2=﹣1﹣或 【解析】试题分析:(1)根据一元二次方程的判别式△=b2﹣4ac的结果判断即可,当△>0时,有两个不相等的实数根,当△=0时,有两个相等的实数根,当△<0时,方程没有实数根; (2)根据一元二次方程根与系数的关系x1+x2=-,x1•x2=,表示出两根的关系,得到x1,x2异号,然后根据绝对值的性质和两根的关系分类讨论即可求解. ...查看答案和解析>>
科目: 来源:人教版九年级数学上册经典试卷 第21章 一元二次方程韦达定理 测试卷 题型:解答题
关于x的方程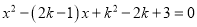 有两个不相等的实数根.
有两个不相等的实数根.
(1)求实数k的取值范围;
(2)设方程的两个实数根分别为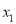 、
、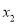 ,存不存在这样的实数k,使得
,存不存在这样的实数k,使得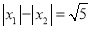 ?若存在,求出这样的k值;若不存在,说明理由.
?若存在,求出这样的k值;若不存在,说明理由.
查看答案和解析>>
科目: 来源:人教版九年级数学上册经典试卷 第21章 一元二次方程韦达定理 测试卷 题型:解答题
已知关于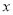 的一元二次方程
的一元二次方程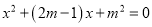 有两个实数根
有两个实数根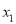 和
和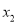 .
.
(1)求实数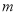 的取值范围;
的取值范围;
(2)当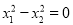 时,求
时,求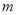 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com