
科目: 来源:2017-2018学年上学期苏州市初三数学期末综合检测 题型:解答题
解方程:
(1) 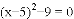 ;
;
(2) 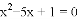 (用配方法);
(用配方法);
(3) 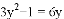
(4) 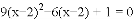
查看答案和解析>>
科目: 来源:2017-2018学年上学期苏州市初三数学期末综合检测 题型:解答题
已知关于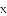
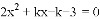 .
.
(1)求证:方程有两个不相等的实数根;
(2)请你给定一个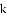
查看答案和解析>>
科目: 来源:2017-2018学年上学期苏州市初三数学期末综合检测 题型:解答题
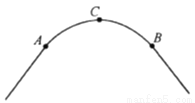
如图,一条公路的转弯处是一段圆弧(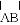 ).
).
(1)用直尺和圆规作出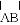 所在圆的圆心
所在圆的圆心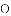
(2)若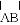 的中点
的中点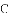
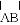 的距离为
的距离为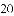
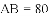
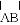 所在圆的半径.
所在圆的半径.
查看答案和解析>>
科目: 来源:2017-2018学年上学期苏州市初三数学期末综合检测 题型:解答题
如图,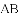
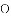
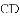
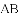
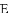
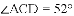
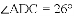
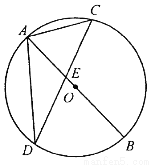
查看答案和解析>>
科目: 来源:2017-2018学年上学期苏州市初三数学期末综合检测 题型:解答题
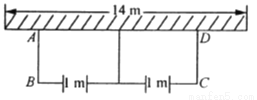
如图,要建一个面积为45 m2的长方形养鸡场(分为两片),养鸡场的一边靠着一面长为14m的墙,另几条边用总长为22 m的竹篱笆围成,每片养鸡场的前面各开一个宽l m的门.求这个养鸡场的长与宽.
查看答案和解析>>
科目: 来源:2017-2018学年上学期苏州市初三数学期末综合检测 题型:解答题
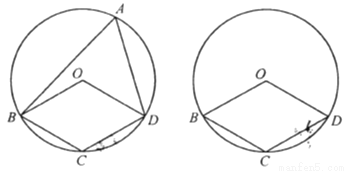
如图,四边形
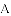
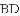
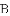
(1)当圆心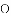
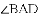
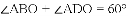
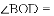
(2)当圆心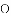
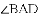
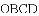
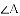
(3)当圆心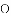
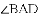
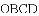
查看答案和解析>>
科目: 来源:2017-2018学年上学期苏州市初三数学期末综合检测 题型:解答题
某批发商以每件50元的价格购进800件T恤,第一个月以单价80元销售,售出了200件;第二个月如果单价不变,预计仍可售出200件,批发商为增加销售量,决定降价销售,根据市场调查,单价每降低1元,可多售出10件,但最低单价应高于购进的价格;第二个月结束后,批发商将对剩余的T恤一次性清仓销售,清仓时单价为40元,设第二个月单价降低x元.
(1)填表:(不需化简)
时间 | 第一个月 | 第二个月 | 清仓时 |
单价(元) | 80 |
| 40 |
销售量(件) | 200 |
|
|
(2)如果批发商希望通过销售这批T恤获利9000元,那么第二个月的单价应是多少元?
(1)第二个月的单价为:80-x,销量为:200+10x,库存为:800-200-(200+10x);(2)70. 【解析】试题分析: (1)80﹣x,200+10x,800﹣200﹣ 时间 第一个月 第二个月 清仓时 单价(元) 80 80﹣x 40 销售量(件) 200 ...查看答案和解析>>
科目: 来源:2017-2018学年上学期苏州市初三数学期末综合检测 题型:解答题
如图,在



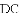





(1)求证:四边形
(2)若
 的度数.
的度数.

查看答案和解析>>
科目: 来源:2017-2018学年上学期苏州市初三数学期末综合检测 题型:解答题
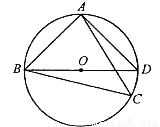
如图,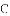
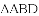
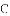
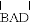 上,且不与点
上,且不与点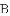
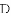
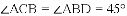
(1)求证: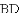
(2)连接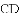
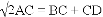 ;
;
(3)若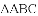
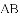
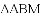
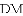
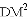 、
、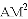 、
、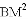 三者之间满足的等量关系,并证明你的结论.
三者之间满足的等量关系,并证明你的结论.
查看答案和解析>>
科目: 来源:2017-2018学年上学期苏州市初三数学期末综合检测 题型:解答题
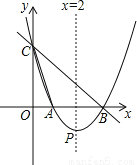
如图,直线y=﹣x+3与x轴,y轴分别相交于点B,C,经过B,C两点的抛物线y=ax2+bx+c与x轴的另一交点为A,顶点为P,且对称轴是直线x=2.
(1)求该抛物线的函数表达式;
(2)请问在抛物线上是否存在点Q,使得以点B,C,Q为顶点的三角形为直角三角形?若存在,请求出点Q的坐标;若不存在,请说明理由;
(3)过S(0,4)的动直线l交抛物线于M,N两点,试问抛物线上是否存在定点T,使得不过定点T的任意直线l都有∠MTN=90°?若存在,请求出点T的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com