
科目: 来源:浙江省宁波市2018届九年级上册期末模拟数学试卷 题型:填空题
用长度一定的绳子围成一个矩形,如果矩形的一边长x(m)与面积y(m2)满足函数关系y=-(x-12)2+144(0<x<24),那么该矩形面积的最大值为________m2 .
144 【解析】∵且, ∴当时,最大=. 即:该矩形面积的最大值为m2.查看答案和解析>>
科目: 来源:浙江省宁波市2018届九年级上册期末模拟数学试卷 题型:填空题
二次函数y=ax2+bx+c(a≠0)的图象如图,对称轴是直线x=1,有以下四个结论:
①abc>0;②b2-4ac>0;③b=-2a;④a+b+c>2.其中正确的是______(填写序号)
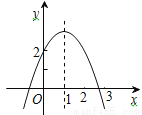
查看答案和解析>>
科目: 来源:浙江省宁波市2018届九年级上册期末模拟数学试卷 题型:填空题
近视眼镜的度数y(度)与镜片焦距x(米)成反比例,已知400度近视镜片的焦距为0.2米,则眼镜度数y与镜片焦距x之间的函数关系式是________.
y= 【解析】由题意可设:, ∵当时,, ∴, ∴与间的函数关系式为:.查看答案和解析>>
科目: 来源:浙江省宁波市2018届九年级上册期末模拟数学试卷 题型:解答题
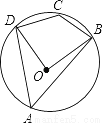
如图,四边形ABCD是⊙O的内接四边形,若∠BOD=88°,求∠BCD的度数.
查看答案和解析>>
科目: 来源:浙江省宁波市2018届九年级上册期末模拟数学试卷 题型:解答题
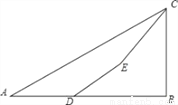
如图,为了测量某建筑物BC的高度,小明先在地面上用测角仪自A处测得建筑物顶部的仰角是30°,然后在水平地而上向建筑物前进了50m到达D处,此时遇到一斜坡,坡度i=1: 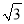 ,沿着斜坡前进20米到达E处测得建筑物顶部的仰角是45°,(坡度i=1:
,沿着斜坡前进20米到达E处测得建筑物顶部的仰角是45°,(坡度i=1: 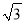 是指坡面的铅直高度FE与水平宽度DE的比).请你计算出该建筑物BC的高度.(取
是指坡面的铅直高度FE与水平宽度DE的比).请你计算出该建筑物BC的高度.(取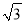 =1.732,结果精确到0.1m).
=1.732,结果精确到0.1m).
查看答案和解析>>
科目: 来源:浙江省宁波市2018届九年级上册期末模拟数学试卷 题型:解答题
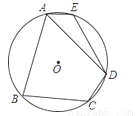
如图,在⊙O的内接四边形ABCD中,AB=AD,∠C=120°,点E在弧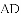
(1)求∠E的度数;
(2)连接OD、OE,当∠DOE=90°时,AE恰好为⊙O的内接正n边形的一边,求n的值
查看答案和解析>>
科目: 来源:浙江省宁波市2018届九年级上册期末模拟数学试卷 题型:解答题
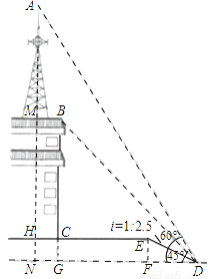
小明在数学课中学习了《解直角三角形》的内容后,双休日组织教学兴趣小组的小伙伴进行实地测量.如图,他们在坡度是i=1:2.5的斜坡DE的D处,测得楼顶的移动通讯基站铁塔的顶部A和楼顶B的仰角分别是60°、45°,斜坡高EF=2米,CE=13米,CH=2米.大家根据所学知识很快计算出了铁塔高AM.亲爱的同学们,相信你也能计算出铁塔AM的高度!请你写出解答过程.(数据 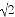 ≈1.41,
≈1.41, 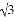 ≈1.73供选用,结果保留整数)
≈1.73供选用,结果保留整数)
查看答案和解析>>
科目: 来源:浙江省宁波市2018届九年级上册期末模拟数学试卷 题型:解答题
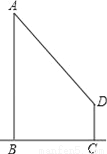
如图,一位同学想利用树影测量树高(AB),他在某一时刻测得高为1m的竹竿影长为0.9m,但当他马上测量树影时,因树靠近一幢建筑物,影子不全落在地面上,有一部分影子在墙上(CD),他先测得留在墙上的影高(CD)为1.2m,又测得地面部分的影长(BC)为2.7m,他测得的树高应为多少米?
查看答案和解析>>
科目: 来源:浙江省宁波市2018届九年级上册期末模拟数学试卷 题型:解答题
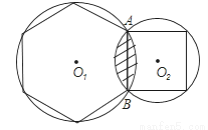
如图,相交两圆的公共弦AB长为120cm,它分别是一圆内接正六边形的边和另一圆内接正方形的边,求两圆相交弧间的阴影部分的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com