
科目: 来源:浙江省宁波市2018届九年级上册期末模拟数学试卷 题型:单选题
直线y=kx经过二、四象限,则抛物线y=kx2+2x+k2图象的大致位置是( )
A. 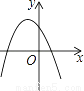 B.
B. 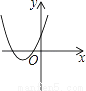 C.
C. 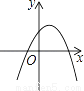 D.
D. 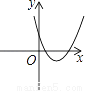
查看答案和解析>>
科目: 来源:浙江省宁波市2018届九年级上册期末模拟数学试卷 题型:单选题
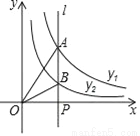
如图,直线l⊥x轴于点P,且与反比例函数y1=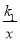 (x>0)及y2=
(x>0)及y2=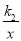 (x>0)的图象分别交于点A,B,连接OA,OB,已知△OAB的面积为2,则k1﹣k2的值为( )
(x>0)的图象分别交于点A,B,连接OA,OB,已知△OAB的面积为2,则k1﹣k2的值为( )
A. 2 B. 3 C. 4 D. ﹣4
C 【解析】试题解析:根据反比例函数k的几何意义可知:△AOP的面积为,△BOP的面积为, ∴△AOB的面积为-, ∴-=2, ∴k1﹣k2=4, 故选C.查看答案和解析>>
科目: 来源:浙江省宁波市2018届九年级上册期末模拟数学试卷 题型:单选题
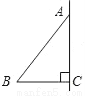
如图,在Rt△ABC中,∠ACB=90°,AC=4,BC=3,将△ABC绕AC所在的直线旋转一周得到一个旋转体,则该旋转体的侧面积为
A. 12π B. 15π C. 30π D. 60π
B 【解析】试题分析:由勾股定理得AB=5,则圆锥的底面周长=6π,旋转体的侧面积=×6π×5=15π.故选B.查看答案和解析>>
科目: 来源:浙江省宁波市2018届九年级上册期末模拟数学试卷 题型:单选题
在Rt△ABC中,∠C=90°,若斜边上的高为h,sinA= , 则AB的长等于( )
, 则AB的长等于( )
A. 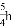 B.
B. 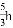 C.
C. 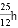 D.
D. 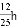
查看答案和解析>>
科目: 来源:浙江省宁波市2018届九年级上册期末模拟数学试卷 题型:单选题
若两个相似三角形的相似比为1∶2,则它们面积的比为()
A. 2∶1 B. 1∶2 C. 1∶4 D. 1∶5
C 【解析】∵两个相似三角形的相似比为1:2, ∴这两个相似三角形的面积比为1:4.查看答案和解析>>
科目: 来源:浙江省宁波市2018届九年级上册期末模拟数学试卷 题型:单选题
如图1,⊙O外接于△ABC,AD为⊙O的直径,∠ABC=30°,则∠CAD=( )
A. 30° B. 40° C. 50° D. 60°

查看答案和解析>>
科目: 来源:浙江省宁波市2018届九年级上册期末模拟数学试卷 题型:填空题
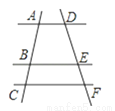
如图,直线AD∥BE∥CF,BC=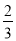 AB,DE=6,那么EF的值是________ .
AB,DE=6,那么EF的值是________ .
查看答案和解析>>
科目: 来源:浙江省宁波市2018届九年级上册期末模拟数学试卷 题型:填空题
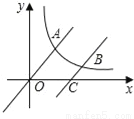
如图,直线y=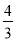 x与双曲线y=
x与双曲线y=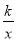 (x>0)交于点A,将直线y=
(x>0)交于点A,将直线y=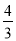 x向下平移个6单位后,与双曲线y=
x向下平移个6单位后,与双曲线y=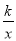 (x>0)交于点B,与x轴交于点C,则C点的坐标为_____;若
(x>0)交于点B,与x轴交于点C,则C点的坐标为_____;若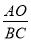 =2,则k=_____.
=2,则k=_____.
查看答案和解析>>
科目: 来源:浙江省宁波市2018届九年级上册期末模拟数学试卷 题型:填空题
写出一个抛物线开口向下,与y轴交于(0,2)点的函数表达式 .
y=﹣x2+x+2(答案不唯一). 【解析】 试题分析:首先根据开口向下得到二次项系数小于0,然后根据与y轴的交点坐标的纵坐标为2得到c ∴c=2,∴抛物线的解析式可以为:y=﹣x2+x+2(答案不唯一). 故答案为:y=﹣x2+x+2(答案不唯一).查看答案和解析>>
科目: 来源:浙江省宁波市2018届九年级上册期末模拟数学试卷 题型:填空题
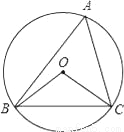
如图,⊙O的半径为4,△ABC是⊙O的内接三角形,连接OB、OC.若∠BAC与∠BOC互补,则弦BC的长为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com