
科目: 来源:2017-2018学年第一学期苏州市八年级数学期末复习综合检测卷 题型:填空题
如图, 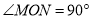 ,已知
,已知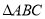 中,
中, 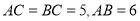 ,
,  的顶点
的顶点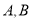 分别在边
分别在边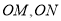 上,当点
上,当点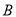 在边
在边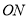 上运动时,点
上运动时,点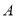 随之在边
随之在边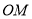 上运动,
上运动, 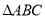 的形状保持不变,在运动过程中,点
的形状保持不变,在运动过程中,点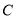 到点
到点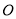 的最大距离为____________.
的最大距离为____________.
查看答案和解析>>
科目: 来源:2017-2018学年第一学期苏州市八年级数学期末复习综合检测卷 题型:解答题
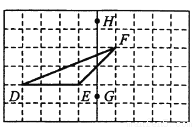
如图,在正方形网格上有一个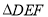 .
.
(1)画 关于直线
关于直线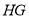 的轴对称图形.
的轴对称图形.
(2)画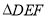 的
的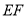 边上的高.
边上的高.
(3)若网格上的最小正方形边长为1,求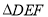 的面积.
的面积.
查看答案和解析>>
科目: 来源:2017-2018学年第一学期苏州市八年级数学期末复习综合检测卷 题型:解答题
中日钓鱼岛争端持续,我国海监船加大钓鱼岛海域的巡航维权力度.如图, 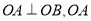 =45海里,
=45海里, 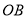 =15海里,钓鱼岛位于
=15海里,钓鱼岛位于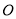 点,我国海监船在点
点,我国海监船在点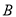 处发现有一不明国籍的渔船,自
处发现有一不明国籍的渔船,自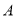 点出发沿着
点出发沿着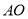 方向匀速驶向钓鱼岛所在地点
方向匀速驶向钓鱼岛所在地点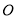 ,我国海监船立即从
,我国海监船立即从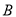 处出发以相同的速度沿某直线去拦截这艘渔船,结果在点
处出发以相同的速度沿某直线去拦截这艘渔船,结果在点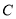 处截住了渔船.
处截住了渔船.
(1)请用直尺和圆规作出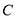 处的位置.
处的位置.
(2)求我国海监船行驶的航程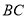 的长.
的长.

查看答案和解析>>
科目: 来源:2017-2018学年第一学期苏州市八年级数学期末复习综合检测卷 题型:解答题
如图, 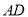 是
是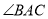 的平分线,点
的平分线,点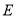 在
在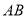 上,且
上,且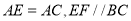 交
交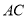 于点
于点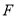 .试说明:
.试说明: 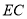 平分
平分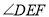 .
.
查看答案和解析>>
科目: 来源:2017-2018学年第一学期苏州市八年级数学期末复习综合检测卷 题型:解答题
已知:如图,在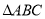 中,
中, 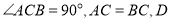 是
是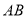 的中点,点
的中点,点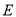 在
在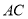 上,点
上,点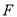 在
在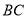 上,且
上,且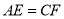 .
.
(1)求证: 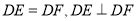 .
.
(2)若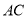 =2,求四边形
=2,求四边形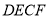 的面积.
的面积.
查看答案和解析>>
科目: 来源:2017-2018学年第一学期苏州市八年级数学期末复习综合检测卷 题型:解答题
如图,在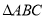 中,
中, 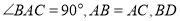 平分
平分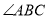 ,
, 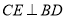 于点
于点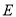 .
.
(1)求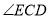 的度数.
的度数.
(2)求证: 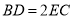 .
.
查看答案和解析>>
科目: 来源:2017-2018学年第一学期苏州市八年级数学期末复习综合检测卷 题型:解答题
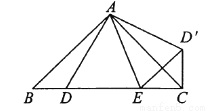
如图,已知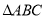 中,
中, 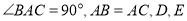 是
是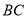 边上的点,将
边上的点,将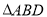 绕点
绕点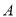 旋转,得到
旋转,得到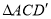 .
.
(1)当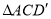 时,求证:
时,求证: 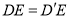 .
.
(2)在(1)的条件下,猜想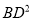 ,
, 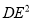 ,
,  有怎样的数量关系,并说明理由.
有怎样的数量关系,并说明理由.
查看答案和解析>>
科目: 来源:2017-2018学年第一学期苏州市八年级数学期末复习综合检测卷 题型:解答题
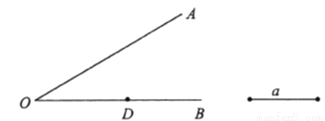
如图,已知 为
为 上的一点,按下列要求进行作图.
上的一点,按下列要求进行作图.
(1)作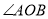 的平分线
的平分线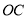 .
.
(2)在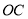 上取一点
上取一点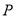 ,使得
,使得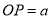 .
.
(3)爱动脑筋的小刚经过仔细观察后,进行如下操作:在边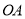 上取一点
上取一点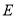 ,使得
,使得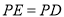 ,这时他发现
,这时他发现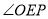 与
与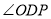 之间存在一定的数量关系,请写出
之间存在一定的数量关系,请写出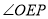 与
与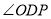 的数量关系,并说明理由.
的数量关系,并说明理由.
查看答案和解析>>
科目: 来源:2017-2018学年第一学期苏州市八年级数学期末复习综合检测卷 题型:解答题
通过类比联想、引申拓展研究典型题目,可达到解一题知一类的目的.下面是一个案例.
原题:如图①,点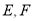 分别在正方形
分别在正方形 的边
的边 上,
上, 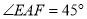 ,连接
,连接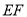 ,则
,则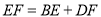 ,试说明理由.
,试说明理由.
(1)思路梳理
因为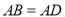 ,所以把
,所以把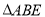 绕点
绕点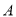 逆时针旋转90°至
逆时针旋转90°至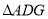 ,可使
,可使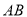 与
与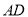 重合.因为
重合.因为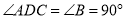 ,所以
,所以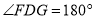 ,点
,点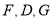 共线.
共线.
根据 ,易证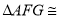 ,得
,得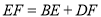 .请证明.
.请证明.
(2)类比引申
如图②,四边形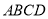 中,
中, 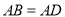 ,
, 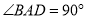 ,点
,点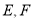 分别在边
分别在边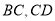 上,
上, 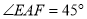 .若
.若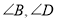 都不是直角,则当
都不是直角,则当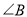 与
与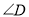 满足等量关系时,
满足等量关系时, 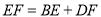 仍然成立,请证明.
仍然成立,请证明.
(3)联想拓展
如图③,在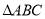 中,
中, 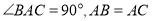 ,点
,点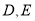 均在边
均在边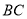 上,且
上,且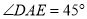 .猜想
.猜想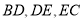 应满足的等量关系,并写出证明过程.
应满足的等量关系,并写出证明过程.
查看答案和解析>>
科目: 来源:吉林省长春市五校2018届九年级(上)期中数学试卷 题型:单选题
方程x2=3x的解是( )
A. x=3 B. x1=0,x2=3 C. x1=0,x2=﹣3 D. x1=1,x2=3
B 【解析】试题分析:移项后分解因式,即可得出两个一元一次方程,求出方程的解即可. x2=3x, x2﹣3x=0, x(x﹣3)=0, x=0,x﹣3=0, x1=0,x2=3, 故选B. 考点: 解一元二次方程-因式分解法.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com