
科目: 来源:浙江省宁波市2018届九年级上册期末模拟数学试卷 题型:填空题
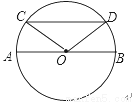
如图,在⊙O中,直径AB∥弦CD,若∠COD=120°,则∠BOD= ________.
查看答案和解析>>
科目: 来源:浙江省宁波市2018届九年级上册期末模拟数学试卷 题型:填空题
挂钟分针的长10cm,经过45分钟,它的针尖转过的弧长是 cm.
. 【解析】 试题分析:分针经过60分钟,转过360°,经过45分钟转过270°, 则分针的针尖转过的弧长是. 故答案是.查看答案和解析>>
科目: 来源:浙江省宁波市2018届九年级上册期末模拟数学试卷 题型:填空题
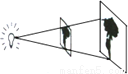
如图,放映幻灯时,通过光源,把幻灯片上的图形放大到屏幕上,若光源到幻灯片的距离为20 cm,到屏幕的距离为60 cm,且幻灯片中图形的高度为6 cm,则屏幕上图形的高度为 cm.
查看答案和解析>>
科目: 来源:浙江省宁波市2018届九年级上册期末模拟数学试卷 题型:填空题
将进货单价为70元的某种商品按零售价100元售出时,每天能卖出20个;若这种商品的零售价在一定范围内每降价2元,其日销售量就增加4个,为了获得最大利润,则售价为________元,最大利润为________元.
90 800 【解析】设降价x元,利润为y, y=(100-70-x)(20+4×) =-2x2+40x+600 =-2(x-10)2+800, 当x=10时,y的最大值为800, 即售价为90元时,最大利润为800元. 故答案为90,800.查看答案和解析>>
科目: 来源:浙江省宁波市2018届九年级上册期末模拟数学试卷 题型:填空题
请写一个图象在第二、四象限的反比例函数解析式: .
(答案不惟一) 【解析】试题分析:因为k<0时,反比例函数的图象在第二、四象限,所以k=-1,k=-2等等都可以,所以答案不唯一,如.查看答案和解析>>
科目: 来源:浙江省宁波市2018届九年级上册期末模拟数学试卷 题型:填空题
若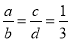 (b+d≠0),则
(b+d≠0),则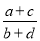 =________
=________
查看答案和解析>>
科目: 来源:浙江省宁波市2018届九年级上册期末模拟数学试卷 题型:填空题
二次函数y=ax2+bx+c(a≠0)自变量x与函数y的对应值如下表:
x | … | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 4 | … |
y | … | m﹣4 | m﹣2 | m﹣ | m | m﹣ | m﹣2 | m﹣4 | … |
若1<m<1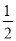 ,则一元二次方程ax2+bx+c=0的两根x1,x2的取值范围是________ .
,则一元二次方程ax2+bx+c=0的两根x1,x2的取值范围是________ .
查看答案和解析>>
科目: 来源:浙江省宁波市2018届九年级上册期末模拟数学试卷 题型:解答题
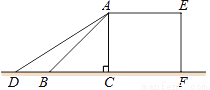
如图,某超市利用一个带斜坡的平台装卸货物,其纵断面ACFE如图所示. AE为台面,AC垂直于地面,AB表示平台前方的斜坡.斜坡的坡角∠ABC为45°,坡长AB为2m.为保障安全,又便于装卸货物,决定减小斜坡AB的坡角,AD 是改造后的斜坡(点D在直线BC上),坡角∠ADC为31°.求斜坡AD底端D与平台AC的距离CD.(结果精确到0.01m)[参考数据:sin31°=0.515,cos31°=0.857,tan31°=0.601, 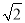 ≈1.414].
≈1.414].
查看答案和解析>>
科目: 来源:浙江省宁波市2018届九年级上册期末模拟数学试卷 题型:解答题
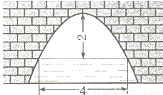
如图,是抛物线形拱桥,当拱顶离水面2米时,水面宽4米.若水面下降1米,则水面宽度将增加多少米?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com