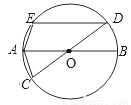
如图，AB、CD是⊙O的直径，AB∥DE，AC=3，则AE=________ ．

3 【解析】试题分析：因为AB∥DE，所以∠BO D=∠D,所以,又∠AO C=∠BOD,所以,所以，所以AE= AC=3．

已知直角三角形两边x、y的长满足|x2-4|+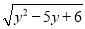=0，则第三边长为 ．

、或． 【解析】 试题分析：∵|x2-4|≥0，， ∴x2-4=0，y2-5y+6=0， ∴x=2或-2（舍去），y=2或3， ①当两直角边是2时，三角形是直角三角形，则斜边的长为：； ②当2，3均为直角边时，斜边为； ③当2为一直角边，3为斜边时，则第三边是直角，长是．

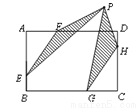
如图，在矩形ABCD中，AD=6，AB=4，点E、G、H、F分别在AB、BC、CD、AD上，且AF=CG=2，BE=DH=1，点P是直线EF、GH之间任意一点，连结PE、PF、PG、PH，则△PEF和△PGH的面积和等于___________.

7

在矩形ABCD中，AD=5，AB=3，点E，F在直线AD上，且四边形BCFE为菱形，若线段EF的中点为点M，则线段AM的长为 ．

6.5，或1.5． 【解析】 试题分析：两种情况：①由矩形的性质得出CD=AB=3，BC=AD=5，∠ADB=∠CDF=90°，由菱形的性质得出CF=EF=BE=BC=5，由勾股定理求出DF，得出MF，即可求出AM；②同①得出AE=4，求出ME，即可得出AM的长． 【解析】 分两种情况：①如图1所示： ∵四边形ABCD是矩形， ∴CD=AB=3，BC=AD=5，∠A...

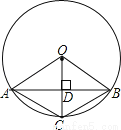
如图，已知在⊙O中，AB是弦，半径OC⊥AB，垂足为点D，要使四边形OACB为菱形，还需要添加一个条件，这个条件可以是 ．

DO=CD． 【解析】 试题分析：利用对角线互相垂直且互相平分的四边形是菱形，进而求出即可． 【解析】 DO=CD．理由如下： ∵在⊙O中，AB是弦，半径OC⊥AB， ∴AD=DB， ∵DO=CD， ∴AD=BD，DO=CD，AB⊥CO， ∴四边形OACB为菱形．

（1）若sinα=0.5138，则锐角α=________ 

（2）若2cosβ=0.7568，则锐角β=________ 

（3）若tanA=37.50，则∠A=________ （结果精确到1〞）

30.92° 67.77° 88°28′12″ 【解析】试题解析：(1)若sinα=0.5138，则锐角 (2)若2cosβ=0.7568，则锐角 (3)若tanA=37.50，则 故答案为：

在矩形纸片ABCD中，AB=16，AD=12，点P在边AB上，若将△DAP沿DP折叠，使点A恰好落在矩形对角线上的点A′处，则AP的长为________．

6或9 【解析】试题解析：①点A落在矩形对角线BD上，如图1所示： ∵AB=16，AD=12， ∴BD=20， 根据折叠的性质, 设AP=x，则BP=16?x， 解得：x=6， ∴AP=6； ②点A落在矩形对角线AC上，如图2所示： 由折叠的性质可知PD垂直平分AA′， ∴∠BAC=∠PDA. ∴tan∠BAC=tan∠PDA. ...

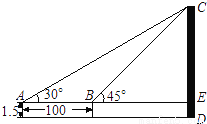
如图，为了测量某建筑物CD的高度，先在地面上用测角仪自A处测得建筑物顶部的仰角是30°，然后在水平地面上向建筑物前进了100m，此时自B处测得建筑物顶部的仰角是45°．已知测角仪的高度是1.5m，请你计算出该建筑物的高度．（取 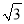=1.732，结果精确到1m）

138m 【解析】试题分析：根据CE=xm，则由题意可知BE=xm，AE=（x+100）m，再利用解直角得出x的值，即可得出CD的长． 试题解析：设CE=xm，则由题意可知BE=xm，AE=（x+100）m． 在Rt△AEC中，tan∠CAE=， 即tan30°=， ∴， 解得x=50+50=136．6， ∴CD=CE+ED=136．6+1．5=138．1...

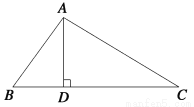
如图，在△ABC中，AD是BC边上的高，tan C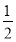＝，AC＝3，AB＝4，求BD的长．(结果保留根号)

【解析】 【解析】 AD是BC边上的高．∴∠ADC＝∠ADB＝90°， 在Rt△ADC中， ∵tan C＝，∴＝. ∴CD＝2AD，∴AD2＋(2AD)2＝(3)2， ∴AD＝3，∴在Rt△ADB中，BD＝＝.

如图，用长为6m的铝合金条制成“日”字形窗框，若窗框的宽为xm，窗户的透光面积为ym2（铝合金条的宽度不计）．

（1）求出y与x的函数关系式；

（2）如何安排窗框的长和宽，才能使得窗户的透光面积最大？并求出此时的最大面积．

（1）y=-x2+3x（0＜x＜2），(2) 窗框的长和宽分别为1.5m和1m时才能使得窗户的透光面积最大，此时的最大面积为1.5m2． 【解析】试题分析：（1）由窗框的宽为x m，则长为m，从而根据矩形面积公式得出函数关系式即可； （2）根据二次函数解析式，用配方法求其最大值即可． 试题解析：（1）根据题意,得（0＜x＜2）. （2）∵,∴当x=1时， . ∴当窗框...