
科目: 来源:江苏省泰州市2017年中考数学二模试卷(解析版) 题型:填空题
点(a﹣1,y1)、(a+1,y2)在反比例函数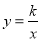 (k>0)的图象上,若y1<y2,则a的范围是 .
(k>0)的图象上,若y1<y2,则a的范围是 .
查看答案和解析>>
科目: 来源:江苏省泰州市2017年中考数学二模试卷(解析版) 题型:填空题
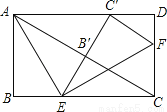
如图,在矩形ABCD中,点E,F分别在BC,CD上,将△ABE沿AE折叠,使点B落在AC上的点B′处,又将△CEF沿EF折叠,使点C落在EB′与AD的交点C′处.则BC:AB的值为 ▲ 。
查看答案和解析>>
科目: 来源:江苏省泰州市2017年中考数学二模试卷(解析版) 题型:解答题
(1)计算:(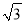 ﹣2)0﹣(﹣1)2017+
﹣2)0﹣(﹣1)2017+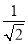 ﹣sin45°;
﹣sin45°;
(2)化简: 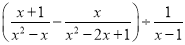 .
.
查看答案和解析>>
科目: 来源:江苏省泰州市2017年中考数学二模试卷(解析版) 题型:解答题
解不等式组 并写出它的非负整数解.
并写出它的非负整数解.
查看答案和解析>>
科目: 来源:江苏省泰州市2017年中考数学二模试卷(解析版) 题型:解答题
为了促进学生多样化发展,某校组织开展了社团活动,分别设置了体育类、艺术类、文学类及其它类社团(要求人人参与社团,每人只能选择一项).为了解学生喜爱哪种社团活动,学校做了一次抽样调查.根据收集到的数据,绘制成如下两幅不完整的统计图,请根据图中提供的信息,完成下列问题:
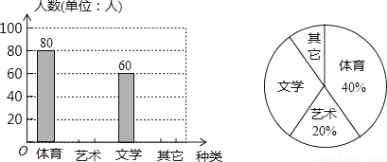
(1)此次共调查了多少人?
(2)求文学社团在扇形统计图中所占圆心角的度数;
(3)请将条形统计图补充完整;
(4)若该校有1500名学生,请估计喜欢体育类社团的学生有多少人?
(1)200;(2)108°;(3)答案见解析;(4)600 【解析】试题分析:(1)根据体育人数80人,占40%,可以求出总人数. (2)根据圆心角=百分比×360°即可解决问题. (3)求出艺术类、其它类社团人数,即可画出条形图. (4)用样本百分比估计总体百分比即可解决问题. 试题解析:(1)80÷40%=200(人). ∴此次共调查20...查看答案和解析>>
科目: 来源:江苏省泰州市2017年中考数学二模试卷(解析版) 题型:解答题
如图的方格地面上,标有编号A、B、C的3个小方格地面是空地,另外6个小方格地面是草坪,除此以外小方格地面完全相同.
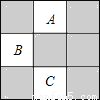
(1)一只自由飞行的鸟,将随意地落在图中的方格地面上,问小鸟落在草坪上的概率是多少?
(2)现从3个小方格空地中任意选取2个种植草坪,则刚好选取A和B的2个小方格空地种植草坪的概率是多少(用树形图或列表法求解)?
(1)P(小鸟落在草坪上) ; (2)列表格列出所有问题的可能的结果见解析,P(编号为A、B的2个小方格空地种植草坪) 【解析】【解析】 (1)P(小鸟落在草坪上) ;(3分) (2)用树状图或列表格列出所有问题的可能的结果: A B C A (A,B) (A,C) B (B,A) (B,C) ...查看答案和解析>>
科目: 来源:江苏省泰州市2017年中考数学二模试卷(解析版) 题型:解答题
已知:如图,在平面直角坐标系xOy中,正比例函数y=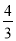 x的图象经过点A,点A的纵坐标为4,反比例函数y=
x的图象经过点A,点A的纵坐标为4,反比例函数y=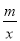 的图象也经过点A,第一象限内的点B在这个反比例函数的图象上,过点B作BC∥x轴,交y轴于点C,且AC=AB.求:
的图象也经过点A,第一象限内的点B在这个反比例函数的图象上,过点B作BC∥x轴,交y轴于点C,且AC=AB.求:
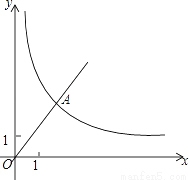
(1)这个反比例函数的解析式;
(2)直线AB的表达式.
(1)y= ;(2)y=﹣x+6. 【解析】试题分析:(1)根据正比例函数的图象经过点,点的纵坐标为4,求出点的坐标,根据反比例函数的图象经过点,求出的值; (2)根据点的坐标和等腰三角形的性质求出点的坐标,运用待定系数法求出直线 的表达式. 试题解析 正比例函数的图象经过点,点的纵坐标为4, ∴点的坐标为(3,4), ∵反比例函数的图象经过点, ∴反比例函数的解析...查看答案和解析>>
科目: 来源:江苏省泰州市2017年中考数学二模试卷(解析版) 题型:解答题
某超市用3 000元购进某种干果销售,由于销售状况良好,超市又调拨9 000元购进该种干果,但这次的进价比第一次的进价提高了20%,购进干果数量比第一次的2倍还多300 kg.如果超市按9元/kg的价格出售,当大部分干果售出后,余下的600 kg按售价的八折售完.
(1)该种干果第一次的进价是多少?
(2)超市销售这种干果共盈利多少元?
(1)该种干果第一次的进价是5元/kg.(2)超市销售这种干果共盈利5820元. 【解析】试题分析:(1)、设第一次进价x元,第二次进价为1.2x,根据题意列出分式方程进行求解;(2)、根据利润=销售额-进价. 试题解析:(1)、设该种干果的第一次进价是每千克x元,则第二次进价是每千克(1+20%)x元, 由题意,得=2×+300, 解得x=5, 经检验x=5是方程的...查看答案和解析>>
科目: 来源:江苏省泰州市2017年中考数学二模试卷(解析版) 题型:解答题
一幢房屋的侧面外墙壁的形状如图所示,它由等腰三角形OCD和矩形ABCD组成,∠OCD=25°,外墙壁上用涂料涂成颜色相同的条纹,其中一块的形状是四边形EFGH,测得FG∥EH,GH=2.6m,∠FGB=65°.
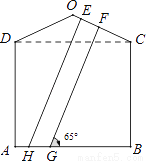
(1)求证:GF⊥OC;
(2)求EF的长(结果精确到0.1m).
(参考数据:sin25°=cos65°≈0.42,cos25°=sin65°≈0.91)
(1)见解析;(2)2.4m. 【解析】试题分析:(1)根据 四边形是矩形, 得出,即可得出答案. (2)根据矩形的判定得出,再利用解直角三角形的知识得出的长. 试题解析:(1)证明:CD与FG交于点M, ∵,四边形ABCD是矩形, ∴ ∴GF⊥CO; (2)作GN⊥EH于点N, ∴四边形ENGF是矩形;查看答案和解析>>
科目: 来源:江苏省泰州市2017年中考数学二模试卷(解析版) 题型:解答题
在△ABC中,D是BC的中点,且AD=AC,DE⊥BC,与AB相交于点E,EC与AD相交于点F.
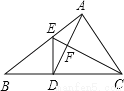
(1)求证:△ABC∽△FCD;
(2)若DE=3,BC=8,求△FCD的面积.
(1)证明见试题解析;(2)4.5. 【解析】 试题分析:(1)利用D是BC边上的中点,DE⊥BC可以得到∠EBC=∠ECB,而由AD=AC可以得到∠ADC=∠ACD,再利用相似三角形的判定,就可以证明题目结论; (2)过点A作AM⊥BC,垂足是M,利用等腰三角形性质求出DM,利用平行线性质定理,求出AM,从而求出△ABC的面积,再利用相似三角形的性质就可以求出三角形FCD的面积...查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com