
科目: 来源:2017年辽宁省营口市大石桥市水源镇中考数学模拟试卷(六) 题型:解答题
某商店经营儿童益智玩具,已知成批购进时的单价是20元.调查发现:销售单价是30元时,月销售量是230件,而销售单价每上涨1元,月销售量就减少10件,但每件玩具售价不能高于40元.设每件玩具的销售单价上涨了x元时(x为正整数),月销售利润为y元.
(1)求y与x的函数关系式并直接写出自变量x的取值范围.
(2)每件玩具的售价定为多少元时,月销售利润恰为2520元?
(3)每件玩具的售价定为多少元时可使月销售利润最大?最大的月利润是多少?
(1)y=﹣10x2+130x+2300( 0<x≤10且x为正整数);(2)每件玩具的售价定为32元时,月销售利润恰为2520元;(3)每件玩具的售价定为36元或37元时,每个月可获得最大利润,最大的月利润是2720元. 【解析】试题分析:(1)由题意可得一件玩具的利润为(30+x-20)元,月销量为(230-10x),根据月利润=一件玩具的利润×月销量即可求出函数关系式; (2)把...查看答案和解析>>
科目: 来源:2017年辽宁省营口市大石桥市水源镇中考数学模拟试卷(六) 题型:解答题
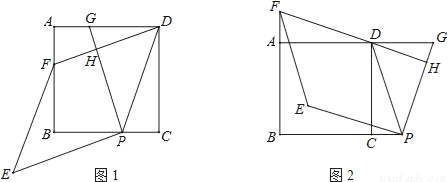
已知,四边形ABCD是正方形,点P在直线BC上,点G在直线AD上(P、G不与正方形顶点重合,且在CD的同侧),PD=PG,DF⊥PG于点H,交直线AB于点F,将线段PG绕点P逆时针旋转90°得到线段PE,连结EF.
(1)如图1,当点P与点G分别在线段BC与线段AD上时.
①求证:DG=2PC;
②求证:四边形PEFD是菱形;
(2)如图2,当点P与点G分别在线段BC与线段AD的延长线上时,请猜想四边形PEFD是怎样的特殊四边形,并证明你的猜想.
查看答案和解析>>
科目: 来源:2017年辽宁省营口市大石桥市水源镇中考数学模拟试卷(六) 题型:解答题
如图,在平面直角坐标系中,直线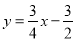 与抛物线
与抛物线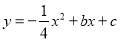 交于A、B两点,点A在x轴上,点B的横坐标为-8.
交于A、B两点,点A在x轴上,点B的横坐标为-8.
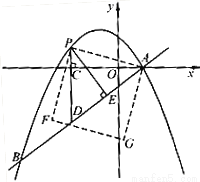
(1)求该抛物线的解析式;
(2)点P是直线AB上方的抛物线上一动点(不与点A、B重合),过点P作x轴的垂线,垂足为C,交直线AB于点D,作PE⊥AB于点E.
①设△PDE的周长为l,点P的横坐标为x,求l关于x的函数关系式,并求出l的最大值;
②连接PA,以PA为边作如图所示一侧的正方形APFG.随着点P的运动,正方形的大小、位置也随之改变.当顶点F或G恰好落在y轴上时,求出对应的点P的坐标.
(1)(2)①15 ② 【解析】试题分析:(1)利用直线解析式求出点A、B的坐标,再利用待定系数法求二次函数解析式解答;(2)①利用直线解析式和抛物线解析式表示出PD,再利用同角的余角相等求出∠DPE=∠BAO,根据直线k值求出∠BAO的正弦和余弦值,然后表示出PE、DE,再根据三角形的周长公式列式整理即可得解,再根据二次函数的最值问题解答;②分(i)点G在y轴上时,过点P作PH⊥x轴于H,...查看答案和解析>>
科目: 来源:山东省2017-2018学年七年级上期末模拟数学试卷 题型:单选题
|a-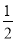 |+(b+1)2=0,则ab的值是( )
|+(b+1)2=0,则ab的值是( )
A. 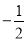 B.
B. 
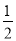 C.
C. 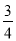 D.
D. 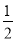
查看答案和解析>>
科目: 来源:山东省2017-2018学年七年级上期末模拟数学试卷 题型:单选题
-(–5)的绝对值是( )
A. 5 B. -5 C. 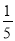 D.
D. 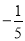
查看答案和解析>>
科目: 来源:山东省2017-2018学年七年级上期末模拟数学试卷 题型:单选题
若2am+2b2n+2与a3b8的和仍是一个单项式,则m与n 的值分别是( )
A. 1,2 B. 2,1 C. 1,1 D. 1,3
D 【解析】【解析】 ∵2am+2b2n+2与a3b8的和仍是一个单项式,∴m+2=3,2n+2=8,解得:m=1,n=3.故选D.查看答案和解析>>
科目: 来源:山东省2017-2018学年七年级上期末模拟数学试卷 题型:单选题
2012年7月第30届奥运会将在伦敦开幕,5个城市的国标标准时间(单位:时)在数轴上表示如图所示,那么伦敦时间2012年7月27日20时应是( )

A. 北京时间2012年7月28日4时 B. 巴黎时间2012年7月27日19时
C. 纽约时间2012年7月28日1时 D. 首尔时间2012年7月28日3时
A 【解析】【解析】 根据数轴,得: A、北京时间是,即2012年7月27日12时,错误; B、巴黎时间是,即2012年7月27日19时,正确; C、纽约时间是,即2012年7月28日1时,错误; D、汉城时间是,即2012年7月27日11时,错误. 故选B.查看答案和解析>>
科目: 来源:山东省2017-2018学年七年级上期末模拟数学试卷 题型:单选题
在一次数学实践探究活动中,大家遇到了这样的问题:
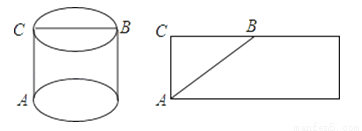
如图,在一个圆柱体形状的包装盒的底部A处有一只壁虎,在顶部B处有一只小昆虫,壁虎沿着什么路线爬行,才能以最短的路线接近小昆虫?
楠楠同学设计的方案是壁虎沿着A﹣C﹣B爬行;
浩浩同学设计的方案是将包装盒展开,在侧面展开图上连接AB,然后壁虎在包装盒的表面上沿着AB爬行.
在这两位同学的设计中,哪位同学的设计是最短路线呢?他们的理论依据是什么?( )
A. 楠楠同学正确,他的理论依据是“直线段最短”
B. 浩浩同学正确,他的理论依据是“两点确定一条直线”
C. 楠楠同学正确,他的理论依据是“垂线段最短”
D. 浩浩同学正确,他的理论依据是“两点之间,线段最短”
D 【解析】【解析】 由题意可得:浩浩同学正确,他的理论依据是“两点之间,线段最短”.故选D.查看答案和解析>>
科目: 来源:山东省2017-2018学年七年级上期末模拟数学试卷 题型:单选题
下列方程中,是一元一次方程的是( )
A. 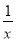 +2=0 B. 3a+6=4a﹣8 C. x2+2x=7 D. 2x﹣7=3y+1
+2=0 B. 3a+6=4a﹣8 C. x2+2x=7 D. 2x﹣7=3y+1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com