
科目: 来源:重庆市2018届2017年秋期期末冲刺卷 题型:解答题
解方程:(1)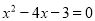 ;(2)
;(2)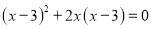
查看答案和解析>>
科目: 来源:重庆市2018届2017年秋期期末冲刺卷 题型:解答题
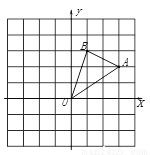
如图,在边长为1的正方形组成的网格中建立直角坐标系,△AOB的顶点均在格点上,点O为原点,点A、B的的坐标分别为A(3,2)、B(1,3).
⑴.请画出将△AOB向左平移3个单位后得到的图形△A1OB1,点B1的坐标为 ;
⑵.请画出将△AOB关于原点O成对称的图形△A2OB2,点A2的坐标为 ;
⑶.在x轴上找一点P,使PA+PB的值最小,则P点的坐标为 .
查看答案和解析>>
科目: 来源:重庆市2018届2017年秋期期末冲刺卷 题型:解答题
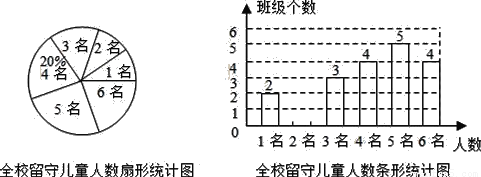
为了解外来务工子女就学情况,某校对七年级各班级外来务工子女的人数情况进行了统计,发现各班级中外来务工子女的人数有1名、2名、3名、4名、5名、6名共六种情况,并制成如下两幅统计图:
(1)求该校七年级平均每个班级有多少名外来务工子女?并将该条形统计图补充完整;
(2)学校决定从只有2名外来务工子女的这些班级中,任选两名进行生活资助,请用列表法或画树状图的方法,求出所选两名外来务工子女来自同一个班级的概率.
查看答案和解析>>
科目: 来源:重庆市2018届2017年秋期期末冲刺卷 题型:解答题
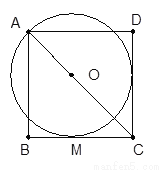
如图,O为正方形ABCD对角线上一点,以O为圆心,OA长为半径的⊙O与BC相切于点M。
(1)求证:CD与⊙O相切;
(2)若正方形ABCD的边长为1,求⊙O的半径。
查看答案和解析>>
科目: 来源:重庆市2018届2017年秋期期末冲刺卷 题型:解答题
“丹棱冻粑”是眉山著名特色小吃,产品畅销省内外,现有一个产品销售点在经销时发现:如果每箱产品盈利10元,每天可售出50箱;若每箱产品涨价1元,日销售量将减少2箱.
(1)现该销售点每天盈利600元,同时又要顾客得到实惠,那么每箱产品应涨价多少元?
(2)若该销售点单纯从经济角度考虑,每箱产品应涨价多少元才能获利最高?
(1)每箱产品应涨价5元.(2)每箱产品应涨价7.5元才能获利最高. 【解析】试题分析:(1)设每箱应涨价x元,得出日销售量将减少2x箱,再由盈利额=每箱盈利×日销售量,依题意得方程求解即可; (2) 设每箱应涨价x元,得出日销售量将减少2x箱,再由盈利额=每箱盈利×日销售量,依题意得函数关系式,进而求出最值. 试题解析:(1) 设每箱应涨价x元, 则每天可售出(50-2x...查看答案和解析>>
科目: 来源:重庆市2018届2017年秋期期末冲刺卷 题型:解答题
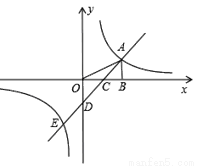
如图,在平面直角坐标系中,点A是反比例函数y=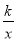 (k≠0)图象上一点,AB⊥x轴于B点,一次函数y=ax+b(a≠0)的图象交y轴于D(0,-2),交x轴于C点,并与反比例函数的图象交于A,E两点,连接OA,若△AOD的面积为4,且点C为OB中点.
(k≠0)图象上一点,AB⊥x轴于B点,一次函数y=ax+b(a≠0)的图象交y轴于D(0,-2),交x轴于C点,并与反比例函数的图象交于A,E两点,连接OA,若△AOD的面积为4,且点C为OB中点.
(1)分别求双曲线及直线AE的解析式;
(2)若点Q在双曲线上,且S△QAB=4S△BAC,求点Q的坐标.
查看答案和解析>>
科目: 来源:重庆市2018届2017年秋期期末冲刺卷 题型:解答题
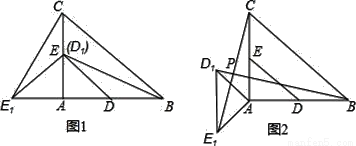
在Rt△ABC中,∠A=90°,AC=AB=4,D,E分别是边AB,AC的中点,若等腰Rt△ADE绕点A逆时针旋转,得到等腰Rt△AD1E1,设旋转角为α(0<α≤180°),记直线BD1与CE1的交点为P.
(1)如图1,当α=90°时,线段BD1的长等于 ,线段CE1的长等于 ;(直接填写结果)
(2)如图2,当α=135°时,求证:BD1=CE1,且BD1⊥CE1.
查看答案和解析>>
科目: 来源:重庆市2018届2017年秋期期末冲刺卷 题型:解答题
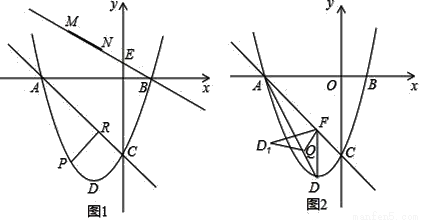
如图1,已知抛物线y=x2+2x﹣3与x轴相交于A,B两点,与y轴交于点C,D为顶点.
(1)求直线AC的解析式和顶点D的坐标;
(2)已知E(0, 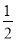 ),点P是直线AC下方的抛物线上一动点,作PR⊥AC于点R,当PR最大时,有一条长为
),点P是直线AC下方的抛物线上一动点,作PR⊥AC于点R,当PR最大时,有一条长为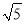 的线段MN(点M在点N的左侧)在直线BE上移动,首尾顺次连接A、M、N、P构成四边形AMNP,请求出四边形AMNP的周长最小时点N的坐标;
的线段MN(点M在点N的左侧)在直线BE上移动,首尾顺次连接A、M、N、P构成四边形AMNP,请求出四边形AMNP的周长最小时点N的坐标;
(3)如图2,过点D作DF∥y轴交直线AC于点F,连接AD,Q点是线段AD上一动点,将△DFQ沿直线FQ折叠至△D1FQ,是否存在点Q使得△D1FQ与△AFQ重叠部分的图形是直角三角形?若存在,请求出AQ的长;若不存在,请说明理由.
查看答案和解析>>
科目: 来源:四川省西昌市2017-2018学年九年级数学(上)期末模拟试卷 题型:单选题
下列电视台的台标,是中心对称图形的是( )
A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目: 来源:四川省西昌市2017-2018学年九年级数学(上)期末模拟试卷 题型:单选题
掷一枚质地均匀的硬币10次,下列说法正确的是( )
A. 必有5次正面朝上 B. 可能有5次正面朝上
C. 掷2次必有1次正面朝上 D. 不可能10次正面朝上
B 【解析】A.不是必然事件,故B错误; B.是随机事件,故C正确; C.不是必然事件,故A错误; D.是随机事件,故D错误; 故选:B.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com