
科目: 来源:2017学年第一学期上海(闵行区)九年级数学质量调研试卷 题型:填空题
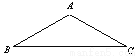
如图,在等腰△ABC中,AB = AC,∠B=30º.以点B为旋转中心,旋转30º,点A、C分别落在点A'、C'处,直线AC、A'C'交于点D,那么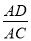 的值为 .
的值为 .
查看答案和解析>>
科目: 来源:2017学年第一学期上海(闵行区)九年级数学质量调研试卷 题型:填空题
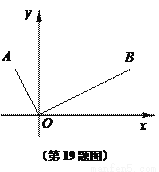
如图在平面直角坐标系xOy中,O为坐标原点,点A的坐标为(-1,2),点B在第一象限,且OB⊥OA,OB=2OA,求经过A、B、O三点的二次函数解析式.
查看答案和解析>>
科目: 来源:2017学年第一学期上海(闵行区)九年级数学质量调研试卷 题型:解答题
如图,已知向量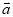 、
、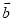 和
和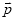 ,求作:
,求作:
(1)向量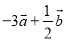 .
.
(2)向量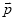 分别在
分别在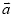 、
、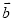 方向上的分向量.
方向上的分向量.

查看答案和解析>>
科目: 来源:2017学年第一学期上海(闵行区)九年级数学质量调研试卷 题型:解答题
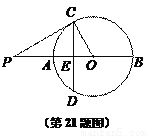
如图,已知OC是⊙O半径,点P在⊙O的直径BA的延长线上,且OC⊥PC,垂足为C.弦CD垂直平分半径AO,垂足为E,PA = 6.
求:(1)⊙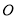 的半径;
的半径;
(2)求弦CD的长.
查看答案和解析>>
科目: 来源:2017学年第一学期上海(闵行区)九年级数学质量调研试卷 题型:解答题
歼-20(英文:Chengdu J-20,绰号:威龙,北约命名:Fire Fang)是我国自主研发的一款单座、双发动机并具备高隐身性、高态势感知、高机动性等能力的第五代战斗机。

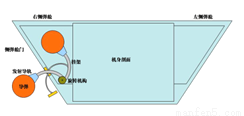
歼-20在机腹部位有一个主弹仓,机身两侧的起落架前方各有一个侧弹仓。歼-20的侧弹舱门为一片式结构,这个弹舱舱门向上开启,弹舱内滑轨的前端向外探出,使导弹头部伸出舱外,再直接点火发射。
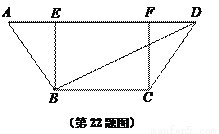
如图是歼-20侧弹舱内部结构图,它的舱体横截面是等腰梯形ABCD,AD//BC,AB = CD,BE⊥AD,CF⊥AD,侧弹舱宽AE = 2.3米,舱底宽BC = 3.94米,舱顶与侧弹舱门的夹角∠A = 53º.
求(1)侧弹舱门AB的长;
(2)舱顶AD与对角线BD的夹角的正切值.(结果精确到0.01,参考数据: 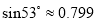 ,
, 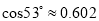 ,
, 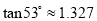 ).
).
查看答案和解析>>
科目: 来源:2017学年第一学期上海(闵行区)九年级数学质量调研试卷 题型:解答题
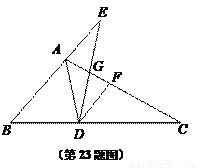
如图,已知在△ABC中,∠BAC =2∠B,AD平分∠BAC,DF//BE,点E在线段BA的延长线上,联结DE,交AC于点G,且∠E =∠C.
(1)求证: 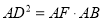 ;
;
(2)求证: 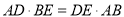 .
.
查看答案和解析>>
科目: 来源:2017学年第一学期上海(闵行区)九年级数学质量调研试卷 题型:解答题
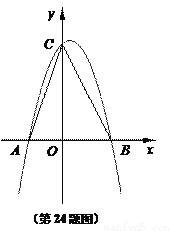
抛物线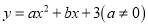 经过点A(
经过点A(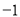 ,0),B(
,0),B(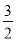 ,0),且与y轴相交于点C.
,0),且与y轴相交于点C.
(1)求这条抛物线的表达式;
(2)求∠ACB的度数;
(3)设点D是所求抛物线第一象限上一点,且在对称轴的右侧,点E在线段AC上,且DE⊥AC,当△DCE与△AOC相似时,求点D的坐标.
查看答案和解析>>
科目: 来源:2017学年第一学期上海(闵行区)九年级数学质量调研试卷 题型:解答题
如图,在Rt△ABC中,∠ACB=90°,AC=4,BC=3,CD是斜边上中线,点E在边AC上,点F在边BC上,且∠EDA=∠FDB,联结EF、DC交于点G.
(1)当∠EDF=90°时,求AE的长;
(2)CE = x,CF = y,求y关于x的函数关系式,并指出x的取值范围;
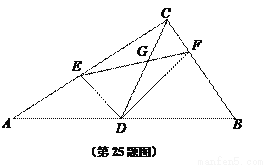
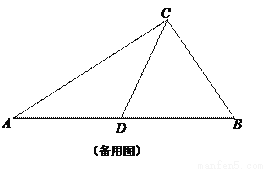
(3)如果△CFG是等腰三角形,求CF与CE的比值.
(1);(2);(3). 【解析】试题分析: 过点E作EH⊥AB于点H,设DH=EH=a,tan∠A=, 得出AH= .在Rt△ABC中,根据勾股定理求出的值,进而求出.根据AH+HD=AD, 即可求得. 分别过点E、F作AB的垂线垂足为H、M,根据CE=x,CF=y,得出AE=4x,CF=3y.进而得到, . , . , .根据tan∠EDA=tan∠FDB.即可得到函数...查看答案和解析>>
科目: 来源:2017年陕西省西安市中考数学模拟试卷 题型:单选题
下列运算正确的是( )
A. (﹣2×3)2=﹣36 B. 22×2﹣2=0
C. (23)2=26 D. 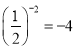
查看答案和解析>>
科目: 来源:2017年陕西省西安市中考数学模拟试卷 题型:单选题
一元二次方程x2﹣2=0的根为( )
A. x=2 B. 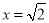 C. x=±2 D.
C. x=±2 D. 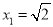 ,
, 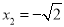
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com