
科目: 来源:2017-2018学年人教版八年级数学下册:期中测评 题型:解答题
已知a,b为一个等腰三角形的两条边长,并满足b=2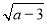 +
+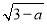 +5,求此等腰三角形的周长.
+5,求此等腰三角形的周长.
查看答案和解析>>
科目: 来源:2017-2018学年人教版八年级数学下册:期中测评 题型:解答题
如图是一个三级台阶,它的每一级的长、宽和高分别等于5 cm,3 cm和1 cm,A和B是这个台阶的两个相对的端点,A点上有一只蚂蚁,想到B点去吃可口的食物.请你想一想,这只蚂蚁从A点出发,沿着台阶面爬到B点,最短线路是多少?
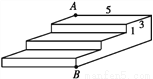
查看答案和解析>>
科目: 来源:2017-2018学年人教版八年级数学下册:期中测评 题型:解答题
已知:如图,在平行四边形ABCD中,AE⊥BD,CF⊥BD,垂足分别为E,F.求证:△ADE≌△CBF .
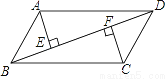
查看答案和解析>>
科目: 来源:2017-2018学年人教版八年级数学下册:期中测评 题型:解答题
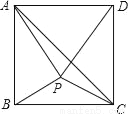
如图,在正方形ABCD内有一点P满足AP=AB,PB=PC,连接AC、PD.
求证:(1)△APB≌△DPC;(2)∠BAP=2∠PAC.
查看答案和解析>>
科目: 来源:2017-2018学年人教版八年级数学下册:期中测评 题型:解答题
如图,在△ABC中,点O是边AC上一个动点,过点O作直线EF∥BC分别交∠ACB、外角∠ACD的平分线于点E,F.
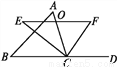
(1)若CE=8,CF=6,求OC的长.
(2)连接AE,AF.问:当点O在边AC上运动到什么位置时,四边形AECF是矩形?并说明理由.
(1)5;(2)四边形AECF是矩形,理由详见解析. 【解析】试题分析:(1)根据平行线的性质以及角平分线的性质得出∠OEC=∠OCE,∠OFC=∠OCF,证出OE=OC=OF,∠ECF=90°,由勾股定理求出EF,即可得出答案; (2)根据平行四边形的判定以及矩形的判定得出即可. 试题解析:(1)证明:∵EF交∠ACB的平分线于点E,交∠ACB的外角平分线于点F,∴∠OCE=∠...查看答案和解析>>
科目: 来源:2017-2018学年人教版八年级数学下册:期中测评 题型:解答题
如图,正方形网格中的每个小正方形边长都是1,每个小格的顶点叫做格点,以格点为顶点分别按下列要求画三角形.
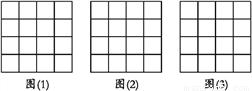
(1)在图(1)中,画一个三角形,使它的三边长都是有理数;
(2)在图(2)中,画一个直角三角形,使它们的三边长都是无理数;
(3)在图(3)中,画一个正方形,使它的面积是10.
详见解析. 【解析】试题分析:(1)画一个边长3,4,5的三角形即可;(2)利用勾股定理,找长为无理数的线段,画三角形即可;(3)画边长为的正方形即可. 试题解析: (1)三边分别为3,4,5(如图(1)); (2)三边分别为 (如图(2)); (3)画一个边长为的正方形(如图(3)).查看答案和解析>>
科目: 来源:山西大学附中2018届九年级10月月考数学试卷 题型:单选题
用配方法解方程 x2-2x-7=0 时,原方程应变形为( )
A. (x+1)2=8 B. (x+2)2=4 C. (x-1)2=8 D. (x-2)2=4
C 【解析】【解析】 方程x2﹣2x﹣7=0,变形得:x2﹣2x=7,配方得:x2﹣2x+1=8,即(x﹣1)2=8,故选C.查看答案和解析>>
科目: 来源:山西大学附中2018届九年级10月月考数学试卷 题型:单选题
若关于x的方程x2+3x+a=0有一个根为-1,则另一个根为( )
A. -2 B. 2 C. 4 D. -3
A 【解析】试题分析:根据一元二次方程根与系数的关系,利用两根和,两根积,即可求出a的值和另一根. 设一元二次方程的另一根为x1,则根据一元二次方程根与系数的关系, 得﹣1+x1=﹣3, 解得:x1=﹣2.查看答案和解析>>
科目: 来源:山西大学附中2018届九年级10月月考数学试卷 题型:单选题
关于x的一元二次方程x2+(m﹣2)x+m+1=0有两个相等的实数根,则m的值是( )
A. 0 B. 8 C. 4±2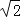 D. 0或8
D. 0或8
查看答案和解析>>
科目: 来源:山西大学附中2018届九年级10月月考数学试卷 题型:单选题
下列命题是真命题的是( )
A. 四边都是相等的四边形是矩形 B. 菱形的对角线相等
C. 对角线互相垂直的平行四边形是正方形 D. 对角线相等的平行四边形是矩形
D 【解析】试题分析:选项A,四边都相等的四边形是菱形,选项A是假命题;选项B,矩形的对角线相等,选项B是假命题;选项C,对角线互相垂直平分且相等的平行四边形是正方形,选项C是假命题;选项D,对角线相等的平行四边形是矩形,选项D是真命题,故选D.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com