
科目: 来源:2017-2018学年度武汉市九年级元月联合测试数学试卷 题型:解答题
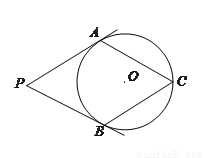
如图, 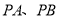 分别与
分别与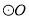 相切于
相切于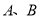 两点,点
两点,点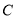 在
在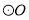 上,∠P=60º,
上,∠P=60º,
(1)求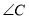 的度数;
的度数;
(2)若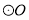 半径为1,求
半径为1,求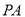 的长.
的长.
查看答案和解析>>
科目: 来源:2017-2018学年度武汉市九年级元月联合测试数学试卷 题型:解答题
三张形状、大小相同但画面不同的风景图片,都按同样的方式剪成相同的三段,然后将上、中、下三段分别混合洗匀,从三堆图片中随机各抽出一张, 求这三张图片恰好组成一张完整风景图片的概率.
【解析】试题分析:设第一张图片剪成的上、中、下三段分别为;设第二张图片剪成的上、中、下三段分别为;设第三张图片剪成的上、中、下三段分别为;根据题意画出树状图,根据概率公式求概率即可. 试题解析: (1)设第一张图片剪成的上、中、下三段分别为; 设第二张图片剪成的上、中、下三段分别为; 设第三张图片剪成的上、中、下三段分别为; 依题意,画树状图如下: 由树状图可知...查看答案和解析>>
科目: 来源:2017-2018学年度武汉市九年级元月联合测试数学试卷 题型:解答题
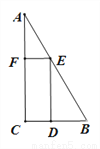
一块三角形材料如图所示, 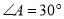 ,
, 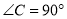 ,
, 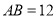 ,用这块材料剪出一个矩形
,用这块材料剪出一个矩形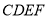 ,其中点
,其中点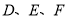 分别在
分别在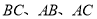 上.设
上.设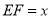 ,请解答下列问题:
,请解答下列问题:
(1)若矩形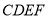 的面积为
的面积为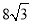 ,求
,求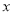 的值;
的值;
(2)矩形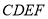 的面积能否为
的面积能否为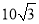 ? 给出你的结论并说明理由.
? 给出你的结论并说明理由.
查看答案和解析>>
科目: 来源:2017-2018学年度武汉市九年级元月联合测试数学试卷 题型:解答题
如图,△ABC内接于 ,
, 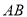 是
是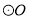 的直径,
的直径, 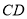 平分
平分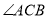 交
交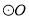 于点
于点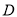 ,交
,交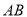 于
于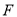 ,弦
,弦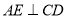 于点
于点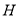 ,连接CE、OH.
,连接CE、OH.
(1)求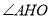 的度数;
的度数;
(2)若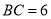 ,
, 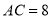 ,求
,求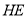 的长.
的长.

查看答案和解析>>
科目: 来源:2017-2018学年度武汉市九年级元月联合测试数学试卷 题型:解答题
某商品现在售价为每件60元,每星期可卖出300件,市场调查反映:调整价格,每件涨价1元,每星期要少卖出10件;每件降价1元,每星期可多卖出20件.已知商品的进价为每件40元.
(1)设每件降价x元,每星期的销售利润为y元;
① 请写出y与x之间的函数关系式;
② 确定x的值,使利润最大,并求出最大利润;
(2)若涨价x元,则x= 元时,利润y的最大值为 元(直接写出答案,不必写过程).
(1)①②x=2或3时y最大为6120;(2)5, 6250 【解析】试题分析:(1)①设每件降价x元,每星期的销售利润为y元,根据等量关系“总利润=每件的利润×每星期的销售量”,写出函数关系式即可;②把函数的解析式化为顶点式,然后根据x取整数,即可求得最大利润;(2)表示出商品的周销售量,根据等量关系“总利润=每件的利润×每星期的销售量”,写出函数关系式,再根据二次函数的性质求出最大利润即...查看答案和解析>>
科目: 来源:2017-2018学年度武汉市九年级元月联合测试数学试卷 题型:解答题
已知△ABC中, 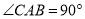 ,
, 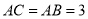 ,△CDE中,
,△CDE中, 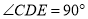 ,CD=DE=5,
,CD=DE=5,
连接接BE,取BE中点F,连接AF、DF.
(1)如图1,若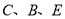 三点共线,
三点共线, 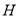 为
为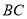 中点.
中点.
①直接指出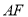 与
与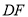 的关系______________;
的关系______________;
②直接指出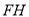 的长度______________;
的长度______________;
(2)将图(1)中的△CDE绕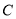 点逆时针旋转
点逆时针旋转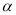 (如图2,
(如图2, 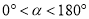 ),试确定
),试确定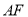 与
与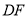 的关系,并说明理由;
的关系,并说明理由;
(3)在(2)中,若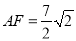 ,请直接指出点
,请直接指出点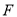 所经历的路径长.
所经历的路径长.
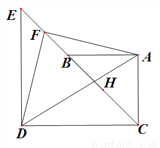
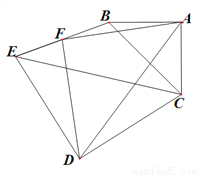
图1 图2
(1)①, ,②;(2), ,理由见解析;(3)或 【解析】试题分析:(1)①如图,过点F M⊥CD于M,FN⊥AC交CA的延长线于点N,根据已知条件易证四边形FMCN为正方形,可得FN=FM,再证△FNA≌△FMD,即可得∠NFA=∠DFM,DF=AF,所以∠NFA+∠AFM=∠DFM+∠AFM=∠DFA=90°,即可证得;②根据勾股定理求得BC=,EC=5 ,因为中点,F为BE的中点,可...查看答案和解析>>
科目: 来源:2017-2018学年度武汉市九年级元月联合测试数学试卷 题型:解答题
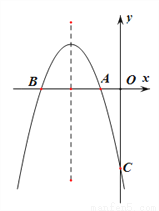
如图,已知抛物线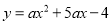 交
交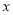 轴于点
轴于点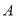 、点
、点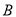 ,交
,交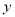 轴于点C,且S△ABC=6.
轴于点C,且S△ABC=6.
(1)求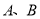 两点的坐标;
两点的坐标;
(2)求△ABC的外接圆与抛物线的对称轴的交点坐标;
(3)点E为抛物线上的一动点(点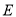 异于
异于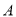 ,且
,且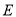 在对称轴右侧),直线
在对称轴右侧),直线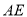 交对称轴于N,
交对称轴于N,
直线BE交对称轴于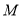 ,对称轴交
,对称轴交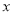 轴于
轴于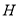 ,试确定
,试确定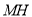 、
、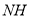 的数量关系并说明理由.
的数量关系并说明理由.
查看答案和解析>>
科目: 来源:云南省2017-2018学年八年级上学期期末考试数学试卷 题型:单选题
下列大学的校徽图案是轴对称图形的是( )

A.清华大学 B.北京大学 C.中国人民大学 D.浙江大学
B. 【解析】 试题分析:A.不是轴对称图形,故错误; B.是轴对称图形,故正确; C.不是轴对称图形,故错误; D.不是轴对称图形,故错误. 故选B.查看答案和解析>>
科目: 来源:云南省2017-2018学年八年级上学期期末考试数学试卷 题型:单选题
在平面直角坐标系xOy中,点P(﹣3,5)关于x轴的对称点的坐标是( )
A. (3,-5) B. (3,5) C. (5,-3) D. (-3,-5)
D 【解析】∵在平面直角坐标系中,关于x轴对称的两点横坐标相等,纵坐标互为相反数, ∴在平面直角坐标系中,点P(-3,5)关于x轴的对称点的坐标为(-3,-5). 故选D.查看答案和解析>>
科目: 来源:云南省2017-2018学年八年级上学期期末考试数学试卷 题型:单选题
已知三角形两边长分别为3和8,则该三角形第三边的长可能是( )
A. 5 B. 10 C. 11 D. 12
B 【解析】试题分析:根据三角形的第三边大于两边之差,而小于两边之和求得第三边的取值范围,再进一步选择. 【解析】 根据三角形的三边关系,得 第三边大于:8﹣3=5,而小于:3+8=11. 则此三角形的第三边可能是:10. 故选:B.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com