
科目: 来源:上海市黄浦区2018届九年级上学期期末调研测试数学试卷(WORD版) 题型:填空题
已知向量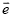 为单位向量,如果向量
为单位向量,如果向量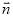 与向量
与向量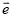 方向相反,且长度为3,那么向量
方向相反,且长度为3,那么向量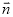 =________.(用单位向量
=________.(用单位向量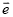 表示)
表示)
查看答案和解析>>
科目: 来源:上海市黄浦区2018届九年级上学期期末调研测试数学试卷(WORD版) 题型:填空题
已知△ABC ∽△DEF,其中顶点A、B、C分别对应顶点D、E、F,如果∠A=40°,∠E=60°,那么∠C=_______度.
80 【解析】因为△ABC ∽△DEF,所以∠A=∠D, ∠B=∠E, ∠C=∠F,因为∠A=40°,∠E=60°, 所以∠B=60°,所以∠C=180°―40°―60°=80°,故答案为: 80.查看答案和解析>>
科目: 来源:上海市黄浦区2018届九年级上学期期末调研测试数学试卷(WORD版) 题型:填空题
已知锐角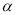 ,满足tan
,满足tan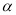 =2,则sin
=2,则sin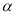 =__________.
=__________.
查看答案和解析>>
科目: 来源:上海市黄浦区2018届九年级上学期期末调研测试数学试卷(WORD版) 题型:填空题
已知点B位于点A北偏东30°方向,点C位于点A北偏西30°方向,且AB=AC=8千米,那么 BC=________千米.
8 【解析】因为点B位于点A北偏东30°方向,点C位于点A北偏西30°方向,所以∠BAC=60°,因为AB=AC,所以△ABC是等边三角形,所以BC=AB=AC=8千米,故答案为:8.查看答案和解析>>
科目: 来源:上海市黄浦区2018届九年级上学期期末调研测试数学试卷(WORD版) 题型:填空题
已知二次函数的图象开口向下,且其图象顶点位于第一象限内,请写出一个满足上述条件的二次函数解析式为_____(表示为y=a(x+m)2+k的形式).
y=﹣(x﹣1)2+1(答案不唯一) 【解析】因为二次函数的顶点坐标为:(-m,k),根据题意图象的顶点位于第一象限,所以可得:m<0,k>0,因此满足m<0,k>0的点即可,故答案为: (答案不唯一).查看答案和解析>>
科目: 来源:上海市黄浦区2018届九年级上学期期末调研测试数学试卷(WORD版) 题型:填空题
已知抛物线y=ax2+bx+c开口向上,一条平行于x轴的直线截此抛物线于M、N两点,那么线段MN的长度随直线向上平移而变_____.(填“大”或“小”)
大 【解析】因为二次函数的开口向上,所以点M,N向上平移时,距离对称轴的距离越大,即MN的长度随直线向上平移而变大,故答案为:大.查看答案和解析>>
科目: 来源:上海市黄浦区2018届九年级上学期期末调研测试数学试卷(WORD版) 题型:填空题
如图,矩形DEFG的边EF在△ABC的边BC上,顶点D、G分别在边AB、AC上.已知AC=6,AB=8,BC=10,设EF=x,矩形DEFG的面积为y,则y关于x的函数关系式为_________.(不必写出定义域)
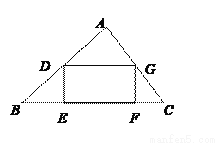
查看答案和解析>>
科目: 来源:上海市黄浦区2018届九年级上学期期末调研测试数学试卷(WORD版) 题型:填空题
如图,在△ABC中,∠C=90°,BC=6,AC=9,将△ABC平移使其顶点C位于△ABC的重心G处,则平移后所得三角形与原△ABC的重叠部分面积是_____.
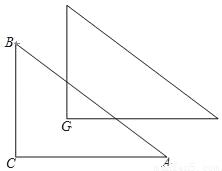
查看答案和解析>>
科目: 来源:上海市黄浦区2018届九年级上学期期末调研测试数学试卷(WORD版) 题型:填空题
如图,点E为矩形ABCD边BC上一点,点F在边CD的延长线上,EF与AC交于点O,若CE:EB=1:2,BC:AB=3:4,AE⊥AF,则CO:OA=_____.
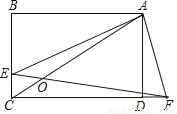
查看答案和解析>>
科目: 来源:上海市黄浦区2018届九年级上学期期末调研测试数学试卷(WORD版) 题型:填空题
如图,平面上七个点A、B、C、D、E、F、G,图中所有的连线长均相等,则cos∠BAF=_____.
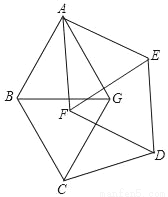
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com