
科目: 来源:安徽省2017~2018学年上学期九年级数学期末试卷 题型:填空题
下列事件:①两直线平行,内错角相等;②掷一枚硬币,国徽的一面朝上,其中,随机事件是______.(填序号)
②. 【解析】 试题解析:①两直线平行,内错角相等是必然事件;②掷一枚硬币,国徽的一面朝上是随机事件.查看答案和解析>>
科目: 来源:安徽省2017~2018学年上学期九年级数学期末试卷 题型:填空题
若x1、x2是方程2x2﹣3x﹣4=0的两个根,则x1•x2+x1+x2的值为 .
【解析】 试题分析:根据题意得x1+x2=,x1•x2=﹣2, 所以x1•x2+x1+x2=﹣2+=﹣.查看答案和解析>>
科目: 来源:安徽省2017~2018学年上学期九年级数学期末试卷 题型:填空题
如图,隧道的截面由抛物线和长方形构成,长方形的长是8m,宽是2m,抛物线的最高点到路面的距离为6米,该抛物线的函数表达式为 ______ .
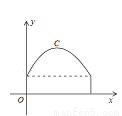
查看答案和解析>>
科目: 来源:安徽省2017~2018学年上学期九年级数学期末试卷 题型:解答题
如图1,⊙O的半径为r(r>0),若点P′在射线OP上,满足OP′•OP=r2,则称点P′是点P关于⊙O的“反演点”.
如图2,⊙O的半径为4,点B在⊙O上,∠BOA=60°,OA=8,若点A′,B′分别是点A,B关于⊙O的反演点,求A′B′的长.
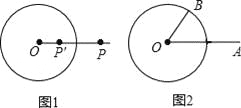
查看答案和解析>>
科目: 来源:安徽省2017~2018学年上学期九年级数学期末试卷 题型:解答题
如图,已知抛物线y=x2+bx+c与x轴交于A,B两点(点A在点B的左侧)与y轴交于点C(0,-3),对称轴是直线x=1,直线BC与抛物线的对称轴交于点D,点E为y轴上一动点,CE的垂直平分线交抛物线于P,Q两点(点P在第三象限)
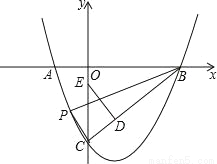
(1)求抛物线的函数表达式和直线BC的函数表达式;
(2)当△CDE是直角三角形,且∠CDE=90° 时,求出点P的坐标;
(3)当△PBC的面积为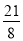 时,求点E的坐标.
时,求点E的坐标.
查看答案和解析>>
科目: 来源:安徽省2017~2018学年上学期九年级数学期末试卷 题型:解答题
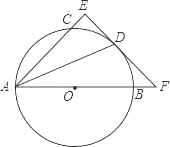
如图,AB是圆O的直径,点C、D在圆O上,且AD平分∠CAB.过点D作AC的垂线,与AC的延长线相交于E,与AB的延长线相交于点F.
求证:EF与圆O相切.
查看答案和解析>>
科目: 来源:安徽省2017~2018学年上学期九年级数学期末试卷 题型:解答题
如图,在平面直角坐标系xOy中,抛物线y=x2+bx+c与y轴交于点C,与x轴交于A,B两点,点B的坐标为(3,0),直线y=﹣x+3恰好经过B,C两点
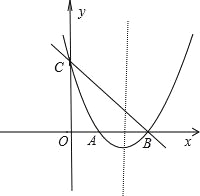
(1)写出点C的坐标;
(2)求出抛物线y=x2+bx+c的解析式,并写出抛物线的对称轴和点A的坐标;
(3)点P在抛物线的对称轴上,抛物线顶点为D且∠APD=∠ACB,求点P的坐标.
(1)C(0,3);(2)y=x2﹣4x+3=(x-1)(x-3),对称轴为x=2,点A(1,0);(3)(2,2)或(2,﹣2) 【解析】 试题分析:(1)由直线y=﹣x+3可求出C点坐标; (2)由B,C两点坐标便可求出抛物线方程,从而求出抛物线的对称轴和A点坐标; (3)作出辅助线OE,由三角形的两个角相等,证明△AEC∽△AFP,根据两边成比例,便可求出PF的长度,...查看答案和解析>>
科目: 来源:安徽省2017~2018学年上学期九年级数学期末试卷 题型:解答题
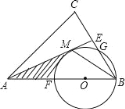
如图,在△ABC中,AB=AC,E是BC中点,点O在AB上,以OB为半径的⊙O经过点AE上的一点M,分别交AB,BC于点F,G,连BM,此时∠FBM=∠CBM.
(1)求证:AM是⊙O的切线;
(2)当BC=6,OB:OA=1:2 时,求 ,AM,AF围成的阴影部分面积.
,AM,AF围成的阴影部分面积.
查看答案和解析>>
科目: 来源:安徽省2017~2018学年上学期九年级数学期末试卷 题型:解答题
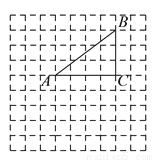
如图,在边长为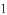 的小正方形组成的网格中,△ABC的三个顶点均在格点上,将△ABC绕点
的小正方形组成的网格中,△ABC的三个顶点均在格点上,将△ABC绕点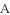 顺时针旋转
顺时针旋转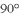 得到△A
得到△A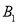
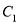 .
.
(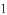 )在网格中画出△A
)在网格中画出△A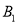
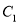 .
.
(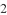 )计算点
)计算点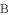 旋转到
旋转到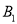 的过程中所经过的路径长.(结果保留
的过程中所经过的路径长.(结果保留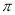 )
)
查看答案和解析>>
科目: 来源:安徽省2017~2018学年上学期九年级数学期末试卷 题型:解答题
袋中有外观相同的红球和白球各1个,随机摸出一球记下颜色,放回摇匀后,再随机摸出一球,求两次摸到球的颜色相同的概率是多少?(先画树状图或列表格,再求概率)
【解析】试题分析:首先根据题意画出树状图,然后由树状图求得所有等可能的结果与小明两次摸出的球颜色相同的情况,再利用概率公式即可求得答案. 试题解析: 画树状图得: ∵共有4种等可能的结果,两次摸到的球的颜色相同的有2种情况, ∴两次摸到的球的颜色相同的概率为: .查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com