
科目: 来源:2017-2018学年九年级数学北师大版上册 第4章 图形的相似 单元测试卷 题型:填空题
如图,若△ADE∽△ACB,且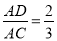 ,若四边形BCED的面积是2,则△ADE的面积是_________.
,若四边形BCED的面积是2,则△ADE的面积是_________.
查看答案和解析>>
科目: 来源:2017-2018学年九年级数学北师大版上册 第4章 图形的相似 单元测试卷 题型:填空题
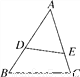
如图,身高为1.7 m的小明AB站在河的一岸,利用树的倒影去测量河对岸一棵树CD的高度,CD在水中的倒影为C′D,A,E,C′在一条线上.已知河BD的宽度为12 m,BE=3 m,则树CD的高为___________.
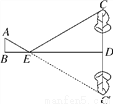
查看答案和解析>>
科目: 来源:2017-2018学年九年级数学北师大版上册 第4章 图形的相似 单元测试卷 题型:填空题
如图,在平面直角坐标系中,△ABC的各顶点坐标为A(-1,1),B(2,3),C(0,3).现以坐标原点为位似中心,作△A′B′C′,使△A′B′C′与△ABC的位似比为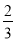 .则点A的对应点A′的坐标为____________.
.则点A的对应点A′的坐标为____________.
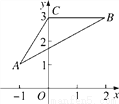
查看答案和解析>>
科目: 来源:2017-2018学年九年级数学北师大版上册 第4章 图形的相似 单元测试卷 题型:解答题
已知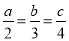 ≠0,2a-b+c=10,求a,b,c的值.
≠0,2a-b+c=10,求a,b,c的值.
查看答案和解析>>
科目: 来源:2017-2018学年九年级数学北师大版上册 第4章 图形的相似 单元测试卷 题型:解答题
图中的两个多边形ABCDEF和A1B1C1D1E1F1相似(各字母已按对应关系排列),∠A=∠D1=135°,∠B=∠E1=120°,∠C1=95°.
(1)求∠F的度数;
(2)如果多边形ABCDEF和A1B1C1D1E1F1的相似比是1:1.5,且CD=15cm,求C1D1的长度.

查看答案和解析>>
科目: 来源:2017-2018学年九年级数学北师大版上册 第4章 图形的相似 单元测试卷 题型:解答题
如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(-2,1),B(-1,4),C(-3,2).
(1)画出△ABC关于y轴对称的图形△A1B1C1,并直接写出点C1的坐标;
(2)以原点O为位似中心,位似比为1∶2,在y轴的左侧,画出△ABC放大后的图形△A2B2C2,并直接写出点C2的坐标;
(3)如果点D(a,b)在线段AB上,请直接写出经过(2)的变化后D的对应点D2的坐标.
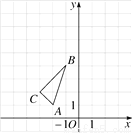
查看答案和解析>>
科目: 来源:2017-2018学年九年级数学北师大版上册 第4章 图形的相似 单元测试卷 题型:解答题
如图,某校数学兴趣小组利用自制的直角三角形硬纸板DEF来测量操场旗杆AB的高度,他们通过调整测量位置,使斜边DF与地面保持平行,并使边DE与旗杆顶点A在同一直线上,已知DE=0.5米,EF=0.25米,目测点D到地面的距离DG=1.5米,到旗杆的水平距离DC=20米,求旗杆的高度.
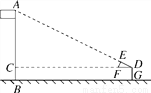
查看答案和解析>>
科目: 来源:2017-2018学年九年级数学北师大版上册 第4章 图形的相似 单元测试卷 题型:解答题
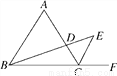
如图,△ABC是等边三角形,CE是∠ACB的外角平分线,点D在AC上,连接BD并延长交CE于点E.
(1)求证:△ABD∽△CED;
(2)若AB=6,AD=2CD,求BE的长.
查看答案和解析>>
科目: 来源:2017-2018学年九年级数学北师大版上册 第4章 图形的相似 单元测试卷 题型:解答题
如图,在△ABC中,点D,E分别在边BC,AB上,BD=AD=AC,AD与CE相交于点F,AE2=EF·EC.
(1)求证:∠ADC=∠DCE+∠EAF;
(2)求证:AF·AD=AB·EF.

查看答案和解析>>
科目: 来源:2017-2018学年九年级数学北师大版上册 第4章 图形的相似 单元测试卷 题型:解答题
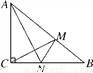
如图,在Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm.动点M从点B出发,在BA边上以每秒3cm的速度向定点A运动,同时动点N从点C出发,在CB边上以每秒2cm的速度向点B运动,运动时间为t秒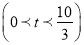 ,连接MN.
,连接MN.
(1)若△BMN与△ABC相似,求t的值;
(2)连接AN,CM,若AN⊥CM,求t的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com