练习册

  • 练习册
  • 试题
    相关习题
     0  321811  321819  321825  321829  321835  321837  321841  321847  321849  321855  321861  321865  321867  321871  321877  321879  321885  321889  321891  321895  321897  321901  321903  321905  321906  321907  321909  321910  321911  321913  321915  321919  321921  321925  321927  321931  321937  321939  321945  321949  321951  321955  321961  321967  321969  321975  321979  321981  321987  321991  321997  322005  366461 

    科目： 来源：广东省汕头市龙湖区2018届九年级上学期期末质量检测数学试卷 题型：单选题

    已知一个圆锥的母线长为30 cm，侧面积为300πcm，则这个圆锥的底面半径为( )

    A. 5 cm B. 10 cm C. 15 cm D. 20 cm

    B 【解析】设这个圆锥的底面半径为r，根据圆锥的侧面积公式可得π×r×30=300π，解得r=10cm，故选B.

    查看答案和解析>>

    科目： 来源：广东省汕头市龙湖区2018届九年级上学期期末质量检测数学试卷 题型：单选题

    如图，铅球运动员掷铅球的高度y(m)与水平距离x(m)之间的函数关系式是y=﹣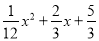，则该运动员此次掷铅球的成绩是(　　)

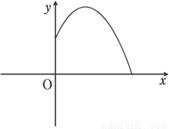
    A. 6m B. 12m C. 8m D. 10m

    D 【解析】试题分析：根据图示，把y=0代入y=-x2+x+可得：-x2+x+=0，解之得：x1=10，x2=-2．又x＞0，解得x=10． 故选D．

    查看答案和解析>>

    科目： 来源：广东省汕头市龙湖区2018届九年级上学期期末质量检测数学试卷 题型：填空题

    方程x2=2x的解为____________．

    x1=0,x2=2 【解析】试题分析：先移项得到x2﹣2x=0，再把方程左边进行因式分解得到x（x﹣2）=0，方程转化为两个一元一次方程：x=0或x﹣2=0，即可得到原方程的解为x1=0，x2=2． 【解析】 ∵x2﹣2x=0， ∴x（x﹣2）=0， ∴x=0或x﹣2=0， ∴x1=0，x2=2． 故答案为x1=0，x2=2．

    查看答案和解析>>

    科目： 来源：广东省汕头市龙湖区2018届九年级上学期期末质量检测数学试卷 题型：填空题

    当x=____时，二次函数 y=﹣2(x﹣1)2﹣5的最大值是______．

    1 ﹣5 【解析】根据二次函数 y=a (x﹣h)2+k的性质可得当x=1时，二次函数 y=﹣2(x﹣1)2﹣5的最大值是-5．

    查看答案和解析>>

    科目： 来源：广东省汕头市龙湖区2018届九年级上学期期末质量检测数学试卷 题型：填空题

    平面直角坐标系中，P(2，3)关于原点对称的点A 坐标是__________.

    (﹣2，﹣3) 【解析】若两个点关于原点对称，则它们的横坐标与纵坐标分别互为相反数. 根据上述规律可知，点P (2, 3)关于原点的对称点A的坐标为(-2, -3). 故本题应填写：(-2, -3).

    查看答案和解析>>

    科目： 来源：广东省汕头市龙湖区2018届九年级上学期期末质量检测数学试卷 题型：填空题

    如图，若点P在反比例函数y=﹣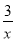 (x＜0)的图象上，过点P作PM⊥x轴于点M，PN⊥y轴于点N，则矩形PMON的面积为____．

    3 【解析】根据反比例函数k的几何意义可得矩形PMON的面积为 .

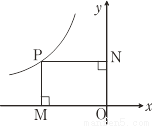
    查看答案和解析>>

    科目： 来源：广东省汕头市龙湖区2018届九年级上学期期末质量检测数学试卷 题型：填空题

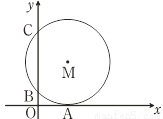
    如图，在平面直角坐标系中，⊙M与x轴相切于点A(8，0)，与y轴分别交于点B(0，4)和点C(0，16)，则圆心M的坐标为________．

    (8，10) 【解析】如图连接BM、OM，AM，作MH⊥BC于H． 已知⊙M与x轴相切于点A（8，0），可得AM⊥OA，OA=8，所以∠OAM=∠MH0=∠HOA=90°，即可判定四边形OAMH是矩形，由矩形的性质可得AM=OH，再由MH⊥BC，由垂径定理得HC=HB=6，即可得AM=10，所以圆心M的坐标为（8，10）．

    查看答案和解析>>

    科目： 来源：广东省汕头市龙湖区2018届九年级上学期期末质量检测数学试卷 题型：填空题

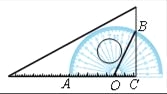
    如图，将一块三角板和半圆形量角器按图中方式叠放，三角板一边与量角器的零刻度线所在直线重合，重叠部分的量角器弧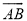（）对应的圆心角（∠AOB）为120°，OC的长为2cm，则三角板和量角器重叠部分的面积为 .

    +2（cm2）. 【解析】试题解析：∵∠AOB=120°， ∴∠BOC=60°， 在Rt△OBC中，OC=2cm，∠BOC=60°， ∴∠OBC=30°， ∴OB=4cm，BC=2cm， 则S扇形OAB= （cm2），S△OBC=OC×BC=2（cm2）， 故S重叠=S扇形OAB+S△OBC=（cm2）．

    查看答案和解析>>

    科目： 来源：广东省汕头市龙湖区2018届九年级上学期期末质量检测数学试卷 题型：解答题

    解方程：(x+3)2=2x+6．

    x1=﹣3,x2=﹣1. 【解析】试题分析：利用因式分解法解方程即可. 试题解析： (x+3)2=2(x+3) , (x+3)2﹣2(x+3)=0 , (x+3)(x+3﹣2)=0, (x+3)(x+1)=0 , ∴x1=﹣3,x2=﹣1.

    查看答案和解析>>

    科目： 来源：广东省汕头市龙湖区2018届九年级上学期期末质量检测数学试卷 题型：解答题

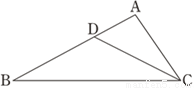
    如图，△ABC中，点D在边AB上，满足∠ACD=∠ABC，若AC=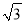，AD=1，求DB的长．

    BD= 2. 【解析】试题分析：根据∠ACD=∠ABC，∠A是公共角，得出△ACD∽△ABC，再利用相似三角形的性质得出AB的长，从而求出DB的长． 试题解析： ∵∠ACD=∠ABC， 又∵∠A=∠A， ∴△ABC∽△ACD ， ∴， ∵AC=，AD=1， ∴， ∴AB=3， ∴BD= AB﹣AD=3﹣1=2 .

    查看答案和解析>>

    同步练习册答案