练习册

  • 练习册
  • 试题
    相关习题
     0  321836  321844  321850  321854  321860  321862  321866  321872  321874  321880  321886  321890  321892  321896  321902  321904  321910  321914  321916  321920  321922  321926  321928  321930  321931  321932  321934  321935  321936  321938  321940  321944  321946  321950  321952  321956  321962  321964  321970  321974  321976  321980  321986  321992  321994  322000  322004  322006  322012  322016  322022  322030  366461 

    科目： 来源：北师大版七年级下册 第一章 整式的乘除 1.6完全平方公式 同步测试 题型：单选题

    为了运用平方差公式计算(2x＋y＋z)(y－2x－z)，下列变形正确的是( )

    A. [2x－(y＋z)]2

    B. [2x＋(y＋z)][2x－(y＋z)]

    C. [y＋(2x＋z)][y－(2x＋z)]

    D. [z＋(2x＋y)][z－(2x＋y)]

    C 【解析】试题解析：根据题意分析：2x、z异号，y同号； ∴（2x+y+z）（y-2x-z）=[y+（2x+z）][y-（2x+z）]； 故选C．

    查看答案和解析>>

    科目： 来源：北师大版七年级下册 第一章 整式的乘除 1.6完全平方公式 同步测试 题型：单选题

    下列计算正确的是（　　）

    A. （x+y）2=x2+y2 B. （x﹣y）2=x2﹣2xy﹣y2

    C. （x+1）（x﹣1）=x2﹣1 D. （x﹣1）2=x2﹣1

    C 【解析】试题分析：根据完全平方公式可得选项A，（x+y）2=x2+y2+2xy，故此选项错误；选项B，（x﹣y）2=x2﹣2xy+y2，故此选项错误；选项D，（x﹣1）2=x2﹣2x+1，故此选项错误；根据平方差公式可得选项C，（x+1）（x﹣1）=x2﹣1，故此选项正确；故答案选C．

    查看答案和解析>>

    科目： 来源：北师大版七年级下册 第一章 整式的乘除 1.6完全平方公式 同步测试 题型：单选题

    下列各式计算结果等于a2b4－2ab2＋1的是( )

    A. (a2b2－1)2 B. (ab2＋1)2

    C. (ab2－1)2 D. (－a2b2－1)2

    C 【解析】试题解析：A. (a2b2－1)2= a4b4－2a2b2＋1, 不符合题意； B. (ab2＋1)2= a2b4+2ab2＋1, 不符合题意； C. (ab2－1)2= a2b4－2ab2＋1,符合题意； D. (－a2b2－1)2 =a4b4－2a2b2＋1, 不符合题意. 故选C.

    查看答案和解析>>

    科目： 来源：北师大版七年级下册 第一章 整式的乘除 1.6完全平方公式 同步测试 题型：单选题

    计算(a＋b－c)(a－b－c)的结果是( )

    A. a2－2ac＋c2－b2 B. a2－b2＋c2

    C. a2－2ab＋b2－c2 D. a2＋b2－c2

    A 【解析】试题解析：原式=[（a-c）+b][（a-c）-b] =（a-c）2-b2 =a2-2ac+c2-b2． 故选A.

    查看答案和解析>>

    科目： 来源：北师大版七年级下册 第一章 整式的乘除 1.6完全平方公式 同步测试 题型：填空题

    计算：（x+1）2﹣（x+2）（x﹣2）=　　．

    2x+5 【解析】 试题分析：原式=x2+2x+1﹣x2+4 =2x+5． 故答案为：2x+5．

    查看答案和解析>>

    科目： 来源：北师大版七年级下册 第一章 整式的乘除 1.6完全平方公式 同步测试 题型：填空题

    若(a－b)2=4，ab=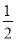，则(a＋b)2=__.

    6 【解析】试题解析：∵（a-b）2=4，ab=， ∴（a-b）2=a2+b2-2ab， =a2+b2-1=4， ∴a2+b2=5， ∴（a+b）2=a2+b2+2ab=5+1=6． 故答案为：6.

    查看答案和解析>>

    科目： 来源：北师大版七年级下册 第一章 整式的乘除 1.6完全平方公式 同步测试 题型：填空题

    若(x＋y)2=9，(x－y)2=5，则xy=__.

    1 【解析】试题解析：（x+y）2=x2+2xy+y2=9 （1）， （x-y）2=x2-2xy+y2=5 （2）， （1）-（2）可得：4xy=4， 解得xy=1． 故答案为：1.

    查看答案和解析>>

    科目： 来源：北师大版七年级下册 第一章 整式的乘除 1.6完全平方公式 同步测试 题型：填空题

    定义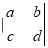为二阶行列式，规定它的运算法则为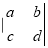=ad－bc.则二阶行列式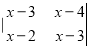的值为___.

    1 【解析】试题解析：由题意可得（x-3）2-（x-2）（x-4）=x2-6x+9-x2+6x-8=1. 故答案为：1.

    查看答案和解析>>

    科目： 来源：北师大版七年级下册 第一章 整式的乘除 1.6完全平方公式 同步测试 题型：解答题

    解方程：3x－4(x－1)(x＋1)=－3－(2x＋2)2.

    x=－1 【解析】试题分析：方程去括号，移项合并，把x系数化为1，即可求出解． 试题解析：3x－4(x－1)(x＋1)=－3－(2x＋2)2. 3x－4x2＋4=－3－4x2-8x-4 ∴11x=-11 ∴x=-1

    查看答案和解析>>

    科目： 来源：北师大版七年级下册 第一章 整式的乘除 1.6完全平方公式 同步测试 题型：解答题

    化简：(a－b)2＋(b－c)2＋(c－a)2/

    2a2＋2b2＋2c2－2ab－2bc－2ac 【解析】试题分析：利用完全平方公式展开，然后合并即可. 试题解析：（a-b）2+（b-c）2+（c-a）2=a2-2ab+b2+b2-2bc+c2+c2-2ac+a2 =2a2+2b2+c2-2ab-2ac-2bc；

    查看答案和解析>>

    同步练习册答案