已知关于x的一元二次方程x2﹣2x+k=0有两个相等的实数根，则k值为 ．

3 【解析】试题解析：根据题意得△=（-2）2-4k=0， 解得k=3．

已知关于x的一元二次方程x2＋(m＋3)x＋m＋1＝0的两个实数根为x1，x2，若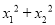＝4，则m的值为___________.

－1或－3 【解析】根据一元二次方程根与系数的关系可得x1+x2=-(m+3), x1·x2=m+1， ＝ 2x1·x2=，解得m=-1或-3.

设一元二次方程x2－3x－1＝0的两根分别是x1，x2，则x1＋x2(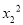－3x2)＝______.

3 【解析】一元二次方程x2－3x－1＝0的一个根是x2，即可得－3x2－1＝0，所以－3x2＝1，再由根与系数的关系可得x1＋x2＝3，所以x1＋x2(－3x2)＝3×1=3.

如图是一个邻边不等的矩形花圃ABCD，它的一边AD利用已有的围墙，另外三边所围的栅栏的总长度是6m.若矩形的面积为4m2，则AB的长度是_____m(可利用的围墙长度超过6m)．

1 【解析】设AB长为x米，则BC长为（6-2x）米． 依题意，得x（6-2x）=4． 整理，得x2-3x+2=0． 解方程，得x1=1，x2=2． 所以当x=1时，6-2x=4； 当x=2时，6-2x=2（不符合题意，舍去）． 答：AB的长为1米；

小明设计了一个魔术盒，当任意实数对(a，b)进入其中时，会得到一个新的实数a2＋2b－3.例如把(2，－5)放入其中就会得到22＋2×(－5)－3＝－9.现将实数对(m，－3m)放入其中，得到实数4，则m＝__________.

7或－1 【解析】根据题意得，m2+2×（-3m）-3=4，解得m1=7，m2=-1，所以m的值为7或-1．

已知关于x的方程x2－(a＋b)x＋ab－1＝0，x1，x2是此方程的两个实数根，现给出三个结论：①x1≠x2；②x1x2＜ab；③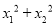＜a2＋b2.则正确结论的序号是______(填序号)．

①② 【解析】Δ＝（a＋b）2－4（ab－1）＝（a－b）2＋4＞0，故方程有两个不相等的实数根，即x1≠x2，故①正确.∵x1·x2＝ab－1＜ab，∴②正确.∵x1＋x2＝a＋b，∴ ＝（x1＋x2）2－2x1x2＝（a＋b）2－2（ab－1）＝a2＋b2＋2＞a2＋b2，故③错误.综上，正确的结论有①②.

解下列方程：

(1)x2＋4x－5＝0；(2)x(x－4)＝2－8x；(3)x－3＝4(x－3)2.

（1）x1＝1，x2＝－5；（2）x1＝－2＋，x2＝－2－；（3）x1＝3，x2＝. 【解析】试题分析：（1）直接利用因式分解法解方程即可；（2）把方程化为一般形式后利用公式法解方程即可；（3）利用因式分解法解方程即可. 试题解析： （1）（x-1）（x+5）=0， x-1=0或x+5=0， ∴x1＝1，x2＝－5； （2）x(x－4)＝2－8x a=1...

已知关于x的方程3x2－(a－3)x－a＝0(a>0)．

(1)求证：方程总有两个不相等的实数根；

(2)若方程有一个根大于2，求a的取值范围．

(1)证明见解析；（2）a>6. 【解析】试题分析：（1）先计算根的判别式得到△=（a＋3）2，然后根据a>0得到△＞0，则可根据判别式的意义得到结论； （2）利用公式法求得方程的两个解为x1＝－1，x2＝，再由方程有一个根大于2，列出不等式，解不等式即可求得a的取值． 试题解析： （1）证明：Δ＝（a－3）2－4×3×（－a）＝（a＋3）2. ∵a>0， ∴（...

2016年2月，某市首条绿道免费公共自行车租赁系统正式启用．市政府在2016年投资了112万元，建成40个公共自行车站点、配置720辆公共自行车．今后将逐年增加投资，用于建设新站点、配置公共自行车．预计2018年将投资340.5万元，新建120个公共自行车站点、配置2205辆公共自行车．

（1）请问每个站点的造价和公共自行车的单价分别是多少万元？

（2）请你求出2016年到2018年市政府配置公共自行车数量的年平均增长率．

（1）每个站点造价为1万元，自行车单价为0.1万元．（2）2016年到2018年市政府配置公共自行车数量的年平均增长率为75%． 【解析】试题分析：（1）设每个站点造价x万元，自行车单价为y万元，根据“资了112万元，建成40个公共自行车站点、配置720辆公共自行车”和“投资340.5万元，新建120个公共自行车站点、配置2205辆公共自行车”两个等量关系列出方程组，解方程组即可；（2）设2...

关于x的一元二次方程x2＋(2k＋1)x＋k2＋1＝0有两个不等实根x1，x2.

(1)求实数k的取值范围；

(2)若方程两实根x1，x2满足|x1|＋|x2|＝x1·x2，求k的值．

(1) k＞；(2)k=2 【解析】试题分析：（1）根据根与系数的关系得出△＞0，代入求出即可； （2）根据根与系数的关系得出x1+x2=﹣（2k+1），x1•x2=k2+1，根据x1+x2=﹣x1•x2得出﹣（2k+1）=﹣（k2+1），求出方程的解，再根据（1）的范围确定即可． 试题解析：（1）∵原方程有两个不相等的实数根， ∴△=（2k+1）2﹣4（k2+1）＞0， ...