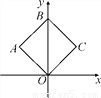
如图，在平面直角坐标系中，正方形OABC的顶点O为坐标原点，点B(0，6)，反比例函数y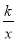＝的图象过点C，则k的值为____．

9 【解析】过点C作CD⊥y轴于点D， ∵正方形OABC的顶点O为坐标原点，点B（0，6）， BD=CD= OB=3， ∴C（3，3）． ∵反比例函数y= 的图象过点C， ∴k=3×3=9．

如图，在△ABC中，D，E分别是边AB，AC上的点，且DE∥BC，若△ADE与△ABC的周长之比为2∶3，AD＝4，则DB＝_______．

2 【解析】由题意得，△ADE 与△ABC 的相似比是2:3， ， 所以， BD=2. 故答案为2.

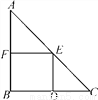
如图，在Rt△ABC中，AB＝BC，∠B＝90°，AC＝10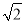，四边形BDEF是△ABC的内接正方形(点D，E，F在三角形的边上)，则此正方形的面积是___．

25 【解析】在Rt△ABC中，AB＝BC，∠B＝90°，AC＝10，根据勾股定理可求得AB=BC=10，可求设EF=x，则AF=10﹣x，由已知EF∥BC，可得到△AFE∽△ABC，根据相似三角形的边对应成比例可得 ，即 ，即可求得x=EF=5，进而根据正方形的面积公式即可求得正方形的面积为25．

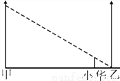
甲、乙两盏路灯底部间的距离是30米，一天晚上，当小华走到距路灯乙底部5米处时，发现自己的身影顶部正好接触路灯乙的底部．已知小华的身高为1.5米，那么路灯甲的高为_____米．

9 【解析】如图，设路灯甲的高为米，由题意和图可得： ，解得， ∴路灯甲的高为9米.

正比例函数y1＝mx(m＞0)的图象与反比例函数y2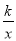＝ (k≠0)的图象交于点A(n，4)和点B，AM⊥y轴，垂足为M.若△AMB的面积为8，则满足y1＞y2的实数x的取值范围是____．

－2＜x＜0或x＞2 【解析】正比例函数y1=mx（m>0）的图象与反比例函数y2=（k≠0）的图象交于点A（n，4）和点B， ∴B（-n，-4）． ∵△AMB的面积为8， ∴×8×n=8， 解得n=2， ∴A（2，4），B（-2，-4）． 由图形可知，当-22时，正比例函数y1=mx（m>0）的图象在反比例函数y2=（k≠0）图象的上方，即...

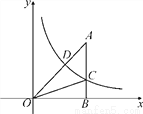
如图，反比例函数y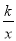＝ (x＞0)的图象交Rt△OAB的斜边OA于点D，交直角边AB于点C，点B在x轴上．若△OAC的面积为5，AD∶OD＝1∶2，则k的值为______．

8 【解析】试题分析：如答图，过D点作x轴的垂线交x轴于H点， ∵△ODH的面积=△OBC的面积= ，△OAC的面积为5，∴△OBA的面积= . ∵AD：OD=1：2，∴OD：OA=2：3. ∵DH∥AB，∴△ODH∽△OAB. ∴，即.解得：k=20．

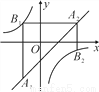
如图，已知点A1，A2，…，An均在直线y＝x－1上，点B1，B2，…，Bn均在双曲线y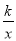＝－上，并且满足A1B1⊥x轴，B1A2⊥y轴，A2B2⊥x轴，B2A3⊥y轴，…，AnBn⊥x轴，BnAn＋1⊥y轴，…，记点An的横坐标为an(n为正整数)．若a1＝－1，则a2018＝___．

2 【解析】∵a1=-1， ∴B1的坐标是（-1，1）， ∴A2的坐标是（2，1）， 即a2=2， ∵a2=2， ∴B2的坐标是（2，-）， ∴A3的坐标是（，-）， 即a3=， ∵a3=， ∴B3的坐标是（，-2）， ∴A4的坐标是（-1，-2）， 即a4=-1， ∵a4=-1， ∴B4的坐标是（-1，1）， ...

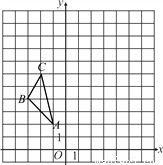
如图，在平面直角坐标系中，已知△ABC三个顶点的坐标分别为A(－1，2)，B(－3，4)，C(－2，6)．

(1)画出△ABC绕点A顺时针旋转90°后得到的△A1B1C1；

(2)以原点O为位似中心，画出将△A1B1C1三条边放大为原来的2倍后的△A2B2C2.

（1）画图见解析；（2）画图见解析. 【解析】试题分析：（1）由A（-1，2），B（-3，4）C（-2，6），可画出△ABC，然后由旋转的性质，即可画出△A1B1C1； （2）由位似三角形的性质，即可画出△A2B2C2． 试题解析：如图：（1）△A1B1C1即为所求； （2）△A2B2C2即为所求．

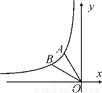
如图，已知反比例函数y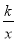＝的图象经过点A(－1， )．

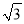(1)试确定此反比例函数的解析式；

(2)点O是坐标原点，将线段OA绕点O逆时针旋转30°后得到线段OB，求出点B的坐标，并判断点B是否在此反比例函数的图象上．

(1)y＝－；(2)点B(－，1)在反比例函数y＝－的图象上. 【解析】试题分析：1）由于反比例函数y=的图象经过点A，运用待定系数法即可求出此反比例函数的解析式；（2）过点A作x轴的垂线交x轴于点C，过点B作x轴的垂线交x轴于点D，由点A的坐标，可求出OA的长度，∠AOC的大小，然后根据旋转的性质得出∠AOB=30°，OB=OA，再求出点B的坐标，进而判断点B是否在此反比例函数的图象上． ...

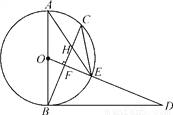
如图，AB是⊙O的直径，点C为⊙O上一点，OF⊥BC于点F，交⊙O于点E，AE与BC交于点H，点D为OE的延长线上一点，且∠ODB＝∠AEC.

求证：(1)BD是⊙O的切线；(2)CE2＝EH·EA.

（1）证明见解析；（2）证明见解析. 【解析】试题分析：（1）由圆周角定理和已知条件证出∠ODB=∠ABC，再证出∠ABC+∠DBF=90°，即∠OBD=90°，即可得出BD是⊙O的切线；（2）连接AC，由垂径定理得出，即可得出∠CAE=∠ECB，再由公共角∠CEA=∠HEC，证明△CEH∽△AEC，得出对应边成比例，即可得出结论. 试题解析：(1)∵∠ODB＝∠AEC，∠AEC＝∠A...