
 某公司投资1200万元购买了一条新生产线生产新产品.根据市场调研,生产每件产品需要成本50元,该产品进入市场后不得低于80元/件且不得超过160元/件,该产品销售量y(万件)与产品售价x(元)之间的关系如图所示.
某公司投资1200万元购买了一条新生产线生产新产品.根据市场调研,生产每件产品需要成本50元,该产品进入市场后不得低于80元/件且不得超过160元/件,该产品销售量y(万件)与产品售价x(元)之间的关系如图所示.分析 (1)设y=kx+b,则由图象可求得k,b,从而得出y与x之间的函数关系式,并写出x的取值范围80≤x≤160;
(2)设公司第一年获利S万元,则可表示出S=-$\frac{1}{10}$(x-150)2-200≤-200,则第一年公司亏损了,当产品售价定为150元/件时,亏损最小,最小亏损为200万元;
(3)假设两年共盈利790万元,则(x-50)(-$\frac{1}{10}$x+25)+(-200)=790,解得x的值在80≤x≤160内.
解答 解:(1)设y=kx+b.由图象可得:$\left\{\begin{array}{l}{80k+b=17}\\{160k+b=9}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-\frac{1}{10}}\\{b=25}\end{array}\right.$.
所以y=-$\frac{1}{10}$x+25,
故x的取值范围是80≤x≤160.
(2)设该公司第一年获利S万元,则
S=(x-50)×y-1200=(x-50)(-$\frac{1}{10}$x+25)-1200
=-$\frac{1}{10}$x2+30x-2450
=-$\frac{1}{10}$(x-150)2-200≤-200,
所以第一年公司是亏损,且当亏损最小时的产品售价为150元/件.
(3)由题意可列方程(x-50)(-$\frac{1}{10}$x+25)+(-200)=790,
解得:x1=140,x2=160.
两个x的值都在80≤x≤160内,
所以第二年售价是140元/件或160/件.
点评 本题是一道一次函数的综合题,考查了二次函数的应用,还考查了用待定系数法求一次函数的解析式.


 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
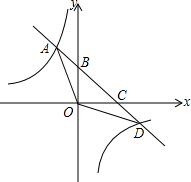 如图,已知在平面直角坐标系xOy中,O是坐标原点,双曲线y1=$\frac{m}{x}$与直线y2=-x+b交于A,D两点,直线y2=-x+b交x轴于点C,交y轴于点B,点B的坐标为(0,3),S△AOB=S△DOC=3.
如图,已知在平面直角坐标系xOy中,O是坐标原点,双曲线y1=$\frac{m}{x}$与直线y2=-x+b交于A,D两点,直线y2=-x+b交x轴于点C,交y轴于点B,点B的坐标为(0,3),S△AOB=S△DOC=3.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
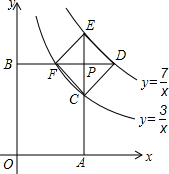 如图,过反比例函数y=$\frac{3}{x}$(x>0)和y=$\frac{7}{x}$(x>0)的图象之间的点P作两坐标轴的垂线,分别交两坐标轴于点A,B,交两函数图象于点C,E,F,D.若四边形OAPB与四边形CDEF都是正方形,则正方形CDEF的面积为$\frac{8}{5}$.
如图,过反比例函数y=$\frac{3}{x}$(x>0)和y=$\frac{7}{x}$(x>0)的图象之间的点P作两坐标轴的垂线,分别交两坐标轴于点A,B,交两函数图象于点C,E,F,D.若四边形OAPB与四边形CDEF都是正方形,则正方形CDEF的面积为$\frac{8}{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
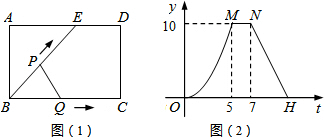
| A. | AE=6cm | B. | sin∠EBC=$\frac{4}{5}$ | ||
| C. | 当0<t≤10时,y=$\frac{2}{5}{t}^{2}$ | D. | 当t=12时,△BPQ是等腰三角形 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com