
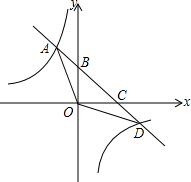
 如图,已知在平面直角坐标系xOy中,O是坐标原点,双曲线y1=$\frac{m}{x}$与直线y2=-x+b交于A,D两点,直线y2=-x+b交x轴于点C,交y轴于点B,点B的坐标为(0,3),S△AOB=S△DOC=3.
如图,已知在平面直角坐标系xOy中,O是坐标原点,双曲线y1=$\frac{m}{x}$与直线y2=-x+b交于A,D两点,直线y2=-x+b交x轴于点C,交y轴于点B,点B的坐标为(0,3),S△AOB=S△DOC=3.分析 (1)由点B在直线y2=-x+b上,得到b=3,于是得到y2=-x+3,设A点的坐标为(x,n),根据S△AOB=3,得到$\frac{1}{2}×3×$|x|=3,x<0,求得A(-2,5),由于y1=$\frac{m}{x}$过点A,于是得到结果;
(2)由y2=-x+3,易得C点坐标为(3,0),同(1)可得,D点坐标为(5,-2),由图象可知,当y1>y2时,-2<x<0或x>5.
解答 解:(1)∵点B在直线y2=-x+b上,
∴b=3,
∴y2=-x+3,
设A点的坐标为(x,n),∵S△AOB=3,
∴$\frac{1}{2}×3×$|x|=3,x<0,
∴x=-2,n=-(-2)+3=5,
∴A(-2,5),
∵y1=$\frac{m}{x}$过点A,∴m=(-2)×5=-10,
所以,m=-10,b=3,
(2)∵y2=-x+3,易得C点坐标为(3,0),
同(1)可得,D点坐标为(5,-2),
由图象可知,当y1>y2时,-2<x<0或x>5.
点评 本题考查了一次函数与反比例函数的交点问题,三角形的面积,正确的识别图形是解题的关键.


科目:初中数学 来源: 题型:解答题
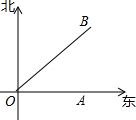 台风中线位于O处洋面上,以40km/h的速度向东北方向移动,在半径为240km的范围内受台风的影响,城市A位于O处的正东方向320km处,问A市是否会遭受此台风的影响?若受影响,求影响时间;若不受影响,请说明理由.(精确到个位)
台风中线位于O处洋面上,以40km/h的速度向东北方向移动,在半径为240km的范围内受台风的影响,城市A位于O处的正东方向320km处,问A市是否会遭受此台风的影响?若受影响,求影响时间;若不受影响,请说明理由.(精确到个位)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 (1)∵∠A+∠B=180°(已知)
(1)∵∠A+∠B=180°(已知)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
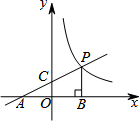 如图,直线y1=$\frac{1}{2}$x+1分别交x轴,y轴于点A,C,点P是直线AC与双曲线y2=$\frac{k}{x}$(x>0)在第一象限内的交点,PB⊥x轴于点B,△PAB的面积为4.
如图,直线y1=$\frac{1}{2}$x+1分别交x轴,y轴于点A,C,点P是直线AC与双曲线y2=$\frac{k}{x}$(x>0)在第一象限内的交点,PB⊥x轴于点B,△PAB的面积为4.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
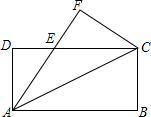 如图,将矩形纸片ABCD沿对角线AC折叠,使点B落到点F的位置,AF与CD交于点E
如图,将矩形纸片ABCD沿对角线AC折叠,使点B落到点F的位置,AF与CD交于点E 查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某公司投资1200万元购买了一条新生产线生产新产品.根据市场调研,生产每件产品需要成本50元,该产品进入市场后不得低于80元/件且不得超过160元/件,该产品销售量y(万件)与产品售价x(元)之间的关系如图所示.
某公司投资1200万元购买了一条新生产线生产新产品.根据市场调研,生产每件产品需要成本50元,该产品进入市场后不得低于80元/件且不得超过160元/件,该产品销售量y(万件)与产品售价x(元)之间的关系如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 里程 | 甲类收费(元) | 乙类收费(元) |
| 3千米以下(包含3千米) | 5.00 | 6.00 |
| 3千米以上,每增加1千米 | 1.60 | 1.30 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某学校体育看台的侧面如图中阴影部分所示,看台有四级高度相等的小台阶,已知看台高为1.6米,现要做一个不锈钢的扶手AB及两根与FG垂直且长度均为0.8米的不锈钢架杆AD和BC(杆子的低端分别为D、C),且∠DAB=66.5°(cos66.5°≈0.4).
某学校体育看台的侧面如图中阴影部分所示,看台有四级高度相等的小台阶,已知看台高为1.6米,现要做一个不锈钢的扶手AB及两根与FG垂直且长度均为0.8米的不锈钢架杆AD和BC(杆子的低端分别为D、C),且∠DAB=66.5°(cos66.5°≈0.4).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com