
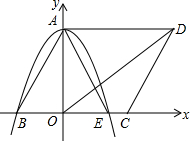
 ИзНјЈ¬ФЪЖҪГжЦұҪЗЧшұкПөЦРЈ¬ЛДұЯРОABCDКЗЖҪРРЛДұЯРОЈ¬ПЯ¶ОAD=6Ј¬¶юҙОәҜКэy=-$\frac{1}{2}$x2-$\frac{1}{6}$x+4УлyЦбҪ»УЪAөгЈ¬УлxЦб·ЦұрҪ»УЪBөгЎўEөгЈЁBөгФЪEөгөДЧуІаЈ©
ИзНјЈ¬ФЪЖҪГжЦұҪЗЧшұкПөЦРЈ¬ЛДұЯРОABCDКЗЖҪРРЛДұЯРОЈ¬ПЯ¶ОAD=6Ј¬¶юҙОәҜКэy=-$\frac{1}{2}$x2-$\frac{1}{6}$x+4УлyЦбҪ»УЪAөгЈ¬УлxЦб·ЦұрҪ»УЪBөгЎўEөгЈЁBөгФЪEөгөДЧуІаЈ©·ЦОц ЈЁ1Ј©·ЦұрҪ«x=0әНy=0ҙъИлҝЙЗуөГAЎўBЎўEөгөДЧшұкЈ»
ЈЁ2Ј©ёщҫЭЧшұкЗуіцAOәНOEөДіӨЈ¬Ҫ«БҪёцЦұҪЗИэҪЗРО¶ФУҰРЎЦұҪЗұЯјЖЛгұИЦөОӘ$\frac{3}{2}$Ј¬¶ФУҰҙуЦұҪЗұЯјЖЛгұИЦөТІКЗ$\frac{3}{2}$Ј¬ЛщТФёщҫЭБҪұЯ¶ФУҰіЙұИАэЈ¬ЗТјРҪЗПаөИЈ¬ЛщТФБҪИэҪЗРОПаЛЖЈ»
ЈЁ3Ј©Ц»РиТӘВъЧгЎчACFОӘөИСьИэҪЗРОЈ¬јҙҝЙХТөҪ¶ФУҰөДБвРОЈ¬ЛщТФ№№ҪЁЎчACFОӘөИСьИэҪЗРОУРЛДЦЦЗйҝцЈәўЩТФAОӘФІРД»ӯФІЈ¬Ҫ»ЦұПЯABУЪF1ЎўF2Ј¬ўЪЧчACөДЦРҙ№ПЯҪ»ЦұПЯABУЪF3Ј¬ўЫТФCОӘФІРДЈ¬ТФACОӘ°лҫ¶Ј¬»ӯФІҪ»ЦұПЯABУЪF4Ј¬АыУГ№ҙ№Й¶ЁАнБРКҪҝЙЗуөГөгFөДЧшұкЈ®
Ҫвҙр ҪвЈәЈЁ1Ј©өұx=0КұЈ¬y=4Ј¬
ЎаAЈЁ0Ј¬4Ј©Ј¬
өұy=0КұЈ¬-$\frac{1}{2}$x2-$\frac{1}{6}$x+4=0Ј¬
2x2+x-24=0Ј¬
ЈЁx+3Ј©ЈЁ3x-8Ј©=0Ј¬
x1=-3Ј¬x2=$\frac{8}{3}$Ј¬
ЎаBЈЁ-3Ј¬0Ј©Ј¬EЈЁ$\frac{8}{3}$Ј¬0Ј©Ј»
ЈЁ2Ј©ЎчAOEУлЎчAODПаЛЖЈ¬АнУЙКЗЈә
ЎЯAЈЁ0Ј¬4Ј©Ј¬
ЎаOA=4Ј¬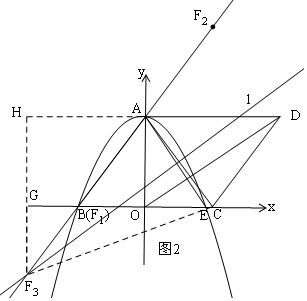
ЎЯEЈЁ$\frac{8}{3}$Ј¬0Ј©Ј¬
ЎаOE=$\frac{8}{3}$Ј¬
Ўа$\frac{AO}{OE}$=$\frac{4}{\frac{8}{3}}$=$\frac{3}{2}$Ј¬$\frac{AD}{AO}=\frac{6}{4}$=$\frac{3}{2}$Ј¬
Ўа$\frac{AO}{OE}=\frac{AD}{AO}$Ј¬
ЎЯЛДұЯРОABCDКЗЖҪРРЛДұЯРОЈ¬
ЎаADЎОBCЈ¬
ЎЯBCЎНAOЈ¬
ЎаADЎНAOЈ¬
ЎаЎПOAD=ЎПAOE=90ЎгЈ¬
ЎаЎчAOEЎЧЎчDAOЈ¬
ЈЁ3Ј©ИзНј2Ј¬ФЪRtЎчAOCЦРЈ¬AC=4Ј¬OC=3Ј¬
ЎаAC=5Ј¬
Н¬АнAB=5Ј¬
ЎаЎчABCКЗөИСьИэҪЗРОЈ¬
ЎаөұFУлBЦШәПКұЈ¬ҙжФЪAЎўCЎўFЎўMОӘ¶ҘөгөДЛДұЯРООӘБвРОЈ¬
јҙF1ЈЁ-3Ј¬0Ј©Ј¬
өұAF2=AB=5КұЈ¬ЎчAF2CКЗөИСьИэҪЗРОЈ¬ҙжФЪAЎўCЎўFЎўMОӘ¶ҘөгөДЛДұЯРООӘБвРОЈ¬
ҙЛКұF2УлB№ШУЪөгA¶ФіЖЈ¬
ЎаF2ЈЁ3Ј¬8Ј©Ј¬
ЙиЦұПЯABөДҪвОцКҪОӘЈәy=kx+bЈ¬
°СAЈЁ0Ј¬4Ј©Ј¬BЈЁ-3Ј¬0Ј©ҙъИлөГЈә$\left\{\begin{array}{l}{-3k+b=0}\\{b=4}\end{array}\right.$Ј¬
ҪвөГЈә$\left\{\begin{array}{l}{k=\frac{4}{3}}\\{b=4}\end{array}\right.$Ј¬
ЎаЦұПЯABөДҪвОцКҪОӘЈәy=$\frac{4}{3}$x+4Ј¬
ИзНј2Ј¬ЧчACөДЦРҙ№ПЯlЈ¬Ҫ»ЦұПЯABУЪF3Ј¬Б¬ҪУF3CЈ¬·Цұр№эAЎўF3ЧчxЦбЎўyЦбөДЖҪРРПЯЈ¬Ҫ»УЪHЈ¬HF3Ҫ»xЦбУЪGЈ¬
ФтAF3=F3CЈ¬
ЙиF3ЈЁxЈ¬$\frac{4}{3}$x+4Ј©Ј¬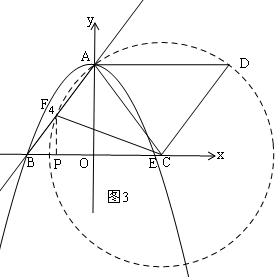
Фт$A{H}^{2}+{F}_{3}{H}^{2}$=$C{G}^{2}+{F}_{3}{G}^{2}$Ј¬
ЈЁ-xЈ©2+ЈЁ4-$\frac{4}{3}$x-4Ј©2=ЈЁ-$\frac{4}{3}$x-4Ј©2+ЈЁ-x+3Ј©2Ј¬
x=-$\frac{75}{14}$Ј¬
өұx=-$\frac{75}{14}$КұЈ¬y=$\frac{4}{3}$ЎБ$ЈЁ-\frac{75}{14}Ј©$+4=-$\frac{22}{7}$Ј¬
ЎаF3ЈЁ-$\frac{75}{14}$Ј¬-$\frac{22}{7}$Ј©Ј»
ИзНј3Ј¬ТФCОӘФІРДЈ¬ТФACОӘ°лҫ¶Ј¬»ӯФІҪ»ЦұПЯABУЪF4Ј¬№эF4ЧчF4PЎНxЦбУЪPЈ¬ФтAC=F4CЈ¬
ЙиF4ЈЁxЈ¬$\frac{4}{3}$x+4Ј©Ј¬
Фт${3}^{2}+{4}^{2}=ЈЁ\frac{4}{3}x+4Ј©^{2}+ЈЁ-x+3Ј©^{2}$Ј¬
$\frac{25}{9}{x}^{2}+\frac{14}{3}x$=0Ј¬
25x2+42x=0Ј¬
xЈЁ25x+42Ј©=0Ј¬
x1=0ЈЁЙбЈ©Ј¬x2=-$\frac{42}{25}$Ј¬
өұx=-$\frac{42}{25}$КұЈ¬y=$\frac{44}{25}$Ј¬
ЎаF4ЈЁ-$\frac{42}{25}$Ј¬$\frac{44}{25}$Ј©Ј¬
ЧЫЙПЛщКцЈ¬FөгөДЧшұкОӘЈәF1ЈЁ-3Ј¬0Ј©Ј¬F2ЈЁ3Ј¬8Ј©Ј¬F3ЈЁ-$\frac{75}{14}$Ј¬-$\frac{22}{7}$Ј©Ј¬F4ЈЁ-$\frac{42}{25}$Ј¬$\frac{44}{25}$Ј©Ј®
өгЖА ұҫМвКЗ¶юҙОәҜКэөДЧЫәПМвЈ¬ҝјІйБЛ¶юҙОәҜКэУлБҪЧшұкЦбөДҪ»өгЎўЖҪРРЛДұЯРОЎўБвРОәНөИСьИэҪЗРОөДРФЦКәНЕР¶ЁЎўПаЛЖИэҪЗРОөДРФЦКәНЕР¶ЁЈ¬ФЪ№№ҪЁөИСьИэҪЗРОКұЈ¬·ЦИэЦЦЗйҝцҪшРРМЦВЫЈ¬ёщҫЭСьіӨПаөИІўУл№ҙ№Й¶ЁАнПаҪбәПБРКҪҪвҫцОКМвЈ®


 З§АпВнЧЯПтјЩЖЪЖЪД©·ВХжКФҫнә®јЩПөБРҙр°ё
З§АпВнЧЯПтјЩЖЪЖЪД©·ВХжКФҫнә®јЩПөБРҙр°ё
| Дкј¶ | ёЯЦРҝОіМ | Дкј¶ | іхЦРҝОіМ |
| ёЯТ» | ёЯТ»Гв·СҝОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СҝОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СҝОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СҝОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СҝОіМНЖјцЈЎ | іхИэ | іхИэГв·СҝОіМНЖјцЈЎ |
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈәСЎФсМв
| AЈ® | 4Ј¬5Ј¬6 | BЈ® | 6Ј¬8Ј¬10 | CЈ® | 7Ј¬24Ј¬25 | DЈ® | 9Ј¬12Ј¬15 |
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈәҪвҙрМв
 ИзНјЈ¬ФЪЖҪГжЦұҪЗПөЦРЈ¬өгAЎўB·ЦұрФЪxЦбЎўyЦбЙПЈ¬AЈЁ8Ј¬0Ј©Ј¬BЈЁ0Ј¬6Ј©Ј¬өгPҙУөгBіц·ўЈ¬СШBAТФГҝГл1ёцөҘО»өДЛЩ¶ИПтөгAФЛ¶ҜЈ¬өгQҙУөгAіц·ўЈ¬СШAOТФГҝГл1ёцөҘО»өДЛЩ¶ИПтөгOФЛ¶ҜЈ¬өгPЎўQН¬Кұіц·ўЈ¬өұөгQөҪҙпөгOКұЈ¬БҪөгН¬КұНЈЦ№ФЛ¶ҜЈ¬ЙиөгQөДФЛ¶ҜКұјдОӘtГлЈ®
ИзНјЈ¬ФЪЖҪГжЦұҪЗПөЦРЈ¬өгAЎўB·ЦұрФЪxЦбЎўyЦбЙПЈ¬AЈЁ8Ј¬0Ј©Ј¬BЈЁ0Ј¬6Ј©Ј¬өгPҙУөгBіц·ўЈ¬СШBAТФГҝГл1ёцөҘО»өДЛЩ¶ИПтөгAФЛ¶ҜЈ¬өгQҙУөгAіц·ўЈ¬СШAOТФГҝГл1ёцөҘО»өДЛЩ¶ИПтөгOФЛ¶ҜЈ¬өгPЎўQН¬Кұіц·ўЈ¬өұөгQөҪҙпөгOКұЈ¬БҪөгН¬КұНЈЦ№ФЛ¶ҜЈ¬ЙиөгQөДФЛ¶ҜКұјдОӘtГлЈ®Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈәМоҝХМв
 ИзНјЈ¬ТСЦӘПЯ¶ОAB=16cmЈ¬өгMФЪABЙПЈ¬AMЈәBM=1Јә3Ј¬PЈ¬Q·ЦұрОӘAMЈ¬ABөДЦРөгЈ¬ФтPQөДіӨОӘ6cmЈ®
ИзНјЈ¬ТСЦӘПЯ¶ОAB=16cmЈ¬өгMФЪABЙПЈ¬AMЈәBM=1Јә3Ј¬PЈ¬Q·ЦұрОӘAMЈ¬ABөДЦРөгЈ¬ФтPQөДіӨОӘ6cmЈ®Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈәҪвҙрМв
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈәҪвҙрМв
 ТСЦӘЈәИзНјЈ¬ЎП1+ЎПD=90ЎгЈ¬BEЎОFCЈ¬ЗТDFЎНBEУлөгGЈ¬Іў·ЦұрУлABЎўCDҪ»УЪөгFЎўDЈ®ЗуЦӨЈәABЎОCDЈ®ЈЁНкіЙЦӨГчІўРҙіцНЖАнТАҫЭЈ©
ТСЦӘЈәИзНјЈ¬ЎП1+ЎПD=90ЎгЈ¬BEЎОFCЈ¬ЗТDFЎНBEУлөгGЈ¬Іў·ЦұрУлABЎўCDҪ»УЪөгFЎўDЈ®ЗуЦӨЈәABЎОCDЈ®ЈЁНкіЙЦӨГчІўРҙіцНЖАнТАҫЭЈ©Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈәСЎФсМв
| AЈ® | 1»т7 | BЈ® | 1»т-7 | CЈ® | -1»т-7 | DЈ® | ЎА1»тЎА7 |
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈәҪвҙрМв
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈәҪвҙрМв
 ИзНјЈәЗуЧчТ»өгPЈ¬К№PM=PNЈ¬ІўЗТК№өгPөҪЎПAOBөДБҪұЯөДҫаАлПаөИЈ®
ИзНјЈәЗуЧчТ»өгPЈ¬К№PM=PNЈ¬ІўЗТК№өгPөҪЎПAOBөДБҪұЯөДҫаАлПаөИЈ®Ійҝҙҙр°ёәНҪвОц>>
№ъјКѧУУЕСЎ - Б·П°ІбБРұн - КФМвБРұн
әюұұКЎ»ҘБӘНшОҘ·ЁәНІ»БјРЕПўҫЩұЁЖҪМЁ | НшЙПУРәҰРЕПўҫЩұЁЧЁЗш | өзРЕХ©ЖӯҫЩұЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРәҰРЕПўҫЩұЁЧЁЗш | ЙжЖуЗЦИЁҫЩұЁЧЁЗш
ОҘ·ЁәНІ»БјРЕПўҫЩұЁөз»°Јә027-86699610 ҫЩұЁУКПдЈә58377363@163.com