
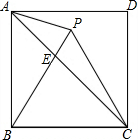
 如图,点P在正方形ABCD内,△PBC是正三角形,AC与PB相交于点E.有以下结论:
如图,点P在正方形ABCD内,△PBC是正三角形,AC与PB相交于点E.有以下结论:分析 根据等边三角形性质得出∠PCB=60°,PC=BC,∠PBC=60°,根据正方形性质和等腰三角形性质求出∠DBC=45°,即可判断①;
根据三角形内角和定理和三角形外角性质求出∠DPC=∠PDC=75°,即可判断②;
根据三角形相似的判定即可判断③;
根据三角形的面积求出△PBC,△DPC,△DBC的面积,即可判断④.
解答 解:∵△PBC是等边三角形,
∴∠PCB=60°,PC=BC,∠PCB=60°,
∵四边形ABCD是正方形,
∴BC=AB,∠ABC=90°,
∴∠ACB=45°,
∴∠ACP=60°-45°=15°,∴①正确;
∵∠ABC=90°,∠PBC=60°,
∴∠ABP=90°-60°=30°,
∵BC=PB,BC=AB,
∴PB=AB,
∴∠BPA=∠PAB=$\frac{1}{2}$(180°-30°)=75°,
∵∠ABP=30°,∠BAC=45°,
∴∠AEP=45°+30°=75°=∠BPA,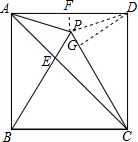
∴AP=AE,
∴△APE为等腰三角形,∴②正确;
∵∠APB=∠APB,∠AEP=∠PAB=75°,
∴△PAE∽△ABP,
∴$\frac{AP}{AB}=\frac{PE}{AP}$,
∴AP2=PE•AB,
∴AE2=PE•AB;∴③正确;
连接PD,过D作DG⊥PC于G,过P作PF⊥AD于F,
设正方形的边长为2a,则S2=4a2,等边三角形PBC的边长为2a,高为$\sqrt{3}$a,
∴PF=2a-$\sqrt{3}$a=(2-$\sqrt{3}$)a,
∴S△APD=$\frac{1}{2}$AD•PF=(2-$\sqrt{3}$)a2,
∴∠PCD=90°-60°=30°,
∴GD=$\frac{1}{2}$CD=$\frac{1}{2}$a,∴S△PCD=$\frac{1}{2}$PC•DG=a2,S△ACD=2a2,
∴S1=S△ACD-S△ADP-S△PCD=2a2-a2-(2-$\sqrt{3}$)a2=($\sqrt{3}$-1)a2<a2,
∴S1:S2≠1:4.
∴④错误;
故答案为:①②③.
点评 本题考查了正方形性质,等边三角形的性质,含30度角的直角三角形,三角形面积,等腰三角形的性质,三角形的内角和定理,相似三角形的判定等知识点的应用,主要考查学生的推理能力,题目是一道中等题.


科目:初中数学 来源: 题型:选择题
 如图,AB是⊙O的直径,AC是⊙O的切线,BC与⊙O相交于D,连接AD、OD(AC≠AB),则能够判断图中∠B的余角(不再添加任何辅助线)的有( )
如图,AB是⊙O的直径,AC是⊙O的切线,BC与⊙O相交于D,连接AD、OD(AC≠AB),则能够判断图中∠B的余角(不再添加任何辅助线)的有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 为了解我省2015届九年级学生学业水平考试体育成绩,现从中随机抽取部分学生的体育成绩进行分段(A:0-29分;B:30-39分;C:40-44分;D:45-49分;E:50分)统计如下:
为了解我省2015届九年级学生学业水平考试体育成绩,现从中随机抽取部分学生的体育成绩进行分段(A:0-29分;B:30-39分;C:40-44分;D:45-49分;E:50分)统计如下:| 分数段 | 人数(人) | 频率 |
| A | 12 | 0.05 |
| B | 36 | b |
| C | 84 | 0.35 |
| D | a | 0.25 |
| E | 48 | 0.2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
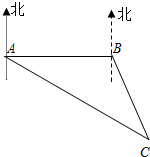 如图,专业救助船“沪救1”轮、“沪救2”轮分别位于A、B两处,同时测得事发地点C在A的南偏东60°且C在B的南偏东30°上.已知B在A的正东方向,且相距100里,请分别求出两艘船到达事发地点C的距离.(注:里是海程单位,相当于一海里.结果保留根号)
如图,专业救助船“沪救1”轮、“沪救2”轮分别位于A、B两处,同时测得事发地点C在A的南偏东60°且C在B的南偏东30°上.已知B在A的正东方向,且相距100里,请分别求出两艘船到达事发地点C的距离.(注:里是海程单位,相当于一海里.结果保留根号)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,直线PA经过点A(-1,0)、点P(1,2),直线PB是一次函数y=-x+3的图象.
如图,直线PA经过点A(-1,0)、点P(1,2),直线PB是一次函数y=-x+3的图象.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com