
分析 正比例函数与反比例函数y=$\frac{4}{x}$的两交点坐标关于原点对称,依此可得x1=-x2,y1=-y2,将(x2-x1)(y2-y1)展开,依此关系即可求解.
解答 解:∵正比例函数的图象与反比例函数y=$\frac{4}{x}$的图象交于A(x1,y1),B(x2,y2)两点,关于原点对称,依此可得x1=-x2,y1=-y2,
∴(x2-x1)(y2-y1)
=x2y2-x2y1-x1y2+x1y1
=x2y2+x2y2+x1y1+x1y1
=4×4
=16.
故答案为:16.
点评 本题考查了反比例函数与正比例函数的交点问题,知道正比例函数与反比例函数的两交点坐标关于原点对称是解题的关键.


 科学实验活动册系列答案
科学实验活动册系列答案科目:初中数学 来源: 题型:解答题
 某体育用品公司以每件60元的批发价购回一批“电子智能跳绳”,第一周以每件120元的价格进行销售,第二周以每件110元的价格进行销售,结果两周共销售该款跳绳100件,两周共实现销售额11400元.
某体育用品公司以每件60元的批发价购回一批“电子智能跳绳”,第一周以每件120元的价格进行销售,第二周以每件110元的价格进行销售,结果两周共销售该款跳绳100件,两周共实现销售额11400元.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
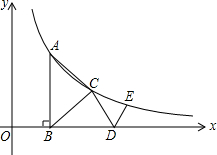 如图,△ABC是等腰直角三角形,斜边AB⊥x轴于B,顶点A,C在反比例函数y=$\frac{2}{x}$(x>0)的图象上,再作等腰Rt△CDE,使直角顶点E在该函数图象上,顶点D在x轴正半轴上,则△CDE的面积是$\frac{11-6\sqrt{3}}{2}$.
如图,△ABC是等腰直角三角形,斜边AB⊥x轴于B,顶点A,C在反比例函数y=$\frac{2}{x}$(x>0)的图象上,再作等腰Rt△CDE,使直角顶点E在该函数图象上,顶点D在x轴正半轴上,则△CDE的面积是$\frac{11-6\sqrt{3}}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
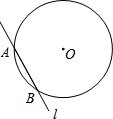 如图,⊙O的半径为1,A为⊙O上一点,过点A的直线l交⊙O于点B,将直线l绕点A旋转180°,当AB的长度由1变为$\sqrt{3}$时,l在圆内扫过的面积为( )
如图,⊙O的半径为1,A为⊙O上一点,过点A的直线l交⊙O于点B,将直线l绕点A旋转180°,当AB的长度由1变为$\sqrt{3}$时,l在圆内扫过的面积为( )| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{3}$或$\frac{π}{2}$+$\sqrt{3}$ | D. | $\frac{π}{6}$或$\frac{π}{2}$+$\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
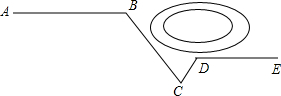 如图,煤气公司安装煤气管道,他们从点A处铺设到点B处时,由于有一个人工湖挡住了去路,需要改变方向经过点C,再拐到点D,然后沿与AB平行的DE方向继续铺设.如图∠BCD=50°,∠ABC=120°,求∠CDE的大小.
如图,煤气公司安装煤气管道,他们从点A处铺设到点B处时,由于有一个人工湖挡住了去路,需要改变方向经过点C,再拐到点D,然后沿与AB平行的DE方向继续铺设.如图∠BCD=50°,∠ABC=120°,求∠CDE的大小.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
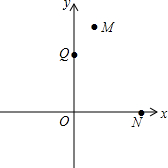 已知,在平面直角坐标系中,点M、N的坐标分别为(1,4)和(3,0),点Q是y轴上的一个动点,且M、N、Q三点不在同一直线上,当△MNQ的周长最小时,求点Q的坐标.
已知,在平面直角坐标系中,点M、N的坐标分别为(1,4)和(3,0),点Q是y轴上的一个动点,且M、N、Q三点不在同一直线上,当△MNQ的周长最小时,求点Q的坐标.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com