练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
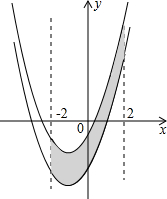
    15．如图，已知抛物线y=x2+2x-3，把此抛物线沿y轴向上平移，平移后的抛物线和原抛物线及直线x=2，x=-2所围成的阴影部分的面积为S，平移的距离为m，则下列图象中，能表示S与m的函数关系的图象大致是（　　）
    A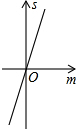．B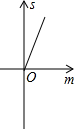．C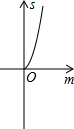．D．

    分析 把阴影部分的面积为S转化为规则图形即可判断．

    解答 解：如图，我们把抛物线沿y轴向上平移，平移后的抛物线和原抛物线及直线x=2，x=-2所围成的阴影部分的面积S可以看做和矩形BB′C′C等积（图形平移后面积不变性），于是可以看出S与m是正比例函数关系，
    故选：B．

    点评 本题主要考查了函数图象与几何变换：由于抛物线平移后的形状不变，因此可把平移后不规则图形转化为规则图形解决问题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

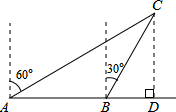    9．如图，一渔船由西往东航行，在A点测得海岛C位于北偏东60°的方向，前进40海里到达B点，此时，测得海岛C位于北偏东30°的方向，则海岛C到航线AB的距离CD是（　　）
    A．20海里B．40海里C．20$\sqrt{3}$海里D．40$\sqrt{3}$海里

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

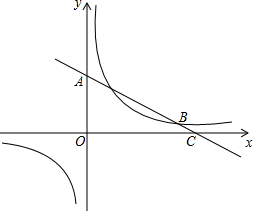    6．如图，在平面直角坐标系中，点A（0，5），C（10，0）在一次函数y=kx+b（b≠0）的图象上，与反比例函数y=$\frac{k′}{x}$（k′≠0）交于点B（8，t）．
    （1）求一次函数和反比例函数的函数关系式；
    （2）将一次函数的图象向下平移m个单位，恰好与反比例函数图象只有一个交点，求m的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

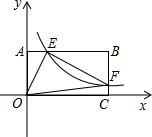    3．如图，将一矩形OABC放在直角坐标系中，O为坐标原点，点A在y轴正半轴上，点E是边AB上的一个动点（不与点A、B重合），过点E的反比例函数y=$\frac{k}{x}$（x＞0）的图象与边BC交与点F．
    （1）若△OAE、△OCF的面积分别为S1、S2，且S1+S2=2，求k的值；
    （2）在（1）的结论下，当OA=2，OC=4时，求三角形OEF的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

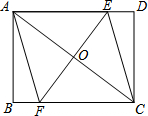    10．如图，矩形ABCD中，对角线AC的垂直平分线交AD、BC于点E、F，AC与EF交于点O，连结AF、CE．
    （1）求证：四边形AFCE是菱形；
    （2）若AB=3，AD=4，求菱形AFCE的边长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    20．已知二次函数y=x2-2x+c（c为常数）．
    （1）若该二次函数的图象与两坐标轴有三个不同的交点，求c的取值范围；
    （2）已知该二次函数的图象与x轴交于点A（-1，0）和点B，与y轴交于点C，顶点为D，若存在点P（m，0）（m＞3）使得△CDP与△BDP面积相等，求m的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．如图，在等边△ABC中：
    （1）在图（1）中，已知点D、E分别在AC、AB上，AE=EB，AD：AC=1：3，求证：△AED∽△CBD；
    （2）在图（2）中，已知点F、G分别在BC、AF上，BF=FC，AG=GF，BG延长线交AC于点D，求证：AD：AC=1：3．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

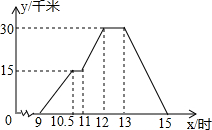    4．李老师周末骑自行车去郊游，如图是他离家的距离y（千米）与时间t（时）之间关系的函数图象，李老师9时离开家，15时到家，根据这个函数图象，请你回答下列问题：
    （1）到达离家最远的地方是什么时间？离家多远？
    （2）他何时开始第一次休息？休息多长时间？
    （3）他从离家最远的地方回家用了多长时间？速度是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    5．若式子$\frac{\sqrt{x-2}}{x-3}$有意义，则x的取值范围为x≥2且x≠3．

    查看答案和解析>>

    同步练习册答案