
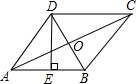
 如图,菱形ABCD的周长为40cm,对角线AC、BD相交于点O,DE⊥AB,垂足为E,DE:AB=4:5,则下列结论:①DE=8cm;②BE=4cm;③BD=4$\sqrt{5}$cm;④AC=8$\sqrt{5}$cm;⑤S菱形ABCD=80cm,正确的有( )
如图,菱形ABCD的周长为40cm,对角线AC、BD相交于点O,DE⊥AB,垂足为E,DE:AB=4:5,则下列结论:①DE=8cm;②BE=4cm;③BD=4$\sqrt{5}$cm;④AC=8$\sqrt{5}$cm;⑤S菱形ABCD=80cm,正确的有( )| A. | ①②④⑤ | B. | ①②③④ | C. | ①③④⑤ | D. | ①②③④⑤ |
分析 由菱形的性质可求得菱形的边长,结合DE:AB=4:5可判断①;在Rt△ABE中由勾股定理可求得AE,则可求得BE,可判断②;在Rt△BDE中由勾股定理可求得BD,可判断③;由菱形的对角线互相平分,可求得BO,在Rt△AOB中可求得AO,可求得AC,可判断④;根据求得的AC和BD可求得菱形的面积,可判断⑤,可得出答案.
解答 解:∵菱形ABCD的周长为40cm,
∴AB=$\frac{1}{4}$×4cm=10cm,
∵DE:AB=4:5,
∴DE=8cm,
故①正确;
∵DE⊥AB,且AD=10cm,DE=8cm,
∴AE=$\sqrt{A{D}^{2}-D{E}^{2}}$=$\sqrt{1{0}^{2}-{8}^{2}}$=6(cm),
∴BE=AB-AE=10cm-6cm=4cm,
故②正确;
∵DE=8cm,BE=4cm,
∴BD=$\sqrt{B{D}^{2}+B{E}^{2}}$=$\sqrt{{8}^{2}+{4}^{2}}$=4$\sqrt{5}$(cm),
故③正确;
∵四边形ABCD是菱形,
∴BO=$\frac{1}{2}$BD=2$\sqrt{5}$cm,且AC⊥BD,
∴AO=$\sqrt{A{B}^{2}-B{O}^{2}}$=$\sqrt{1{0}^{2}-(2\sqrt{5})^{2}}$=4$\sqrt{5}$(cm),
∴AC=2AO=8$\sqrt{5}$cm,
故④正确;
∴S菱形ABCD=$\frac{1}{2}$AC•BD=$\frac{1}{2}$×8$\sqrt{5}$×4$\sqrt{5}$=80(cm2),
故⑤不正确,单位错误;
∴正确的为①②③④,
故选B.
点评 本题主要考查菱形的性质,掌握菱形的四边相等、对角线互相垂直且平分是解题的关键.注意菱形面积公式的应用.


科目:初中数学 来源: 题型:选择题
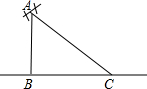 如图所示,有一根高为16米的电线杆A处断裂,电线杆顶部C落在高电线杆底部B点8米远的地方,则电线杆断裂处A离地面的距离AB的长为( )
如图所示,有一根高为16米的电线杆A处断裂,电线杆顶部C落在高电线杆底部B点8米远的地方,则电线杆断裂处A离地面的距离AB的长为( )| A. | 6米 | B. | 7米 | C. | 8米 | D. | 9米 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{5{x}^{2}}$ | B. | $\sqrt{0.9}$ | C. | $\sqrt{\frac{3}{7}}$ | D. | $\sqrt{{a}^{2}-3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{3}+\sqrt{2}=\sqrt{5}$ | B. | $3\sqrt{2}-2\sqrt{2}=1$ | C. | $\sqrt{3^2}=3$ | D. | $\sqrt{9}=±3$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
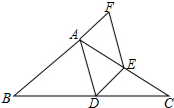 如图,△ABC中,点D,E分别是边BC,AC的中点,连接DE,AD,点F在BA的延长线上,且AF=$\frac{1}{2}$AB,连接EF,判断四边形ADEF的形状,并加以证明.
如图,△ABC中,点D,E分别是边BC,AC的中点,连接DE,AD,点F在BA的延长线上,且AF=$\frac{1}{2}$AB,连接EF,判断四边形ADEF的形状,并加以证明.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com