练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    3．化简$\sqrt{（2a-1）^{2}}$-（$\sqrt{2a-3}$）2的结果是（　　）
    A．2B．4-4aC．-2D．4a-4

    分析 直接利用二次根式的性质得出2a-3≥0，则2a-1＞0，进而化简求出答案．

    解答 解：∵$\sqrt{2a-3}$有意义，
    ∴2a-3≥0，则2a-1＞0，
    ∴$\sqrt{（2a-1）^{2}}$-（$\sqrt{2a-3}$）2=2a-1-（2a-3）=2．
    故选：A．

    点评 此题主要考查了二次根式的性质与化简，正确得出各项符号是解题关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    13．如图是甲、乙两公司近年销售收入情况的折线统计图，根据统计图得出下列结论，其中正确的是（　　）
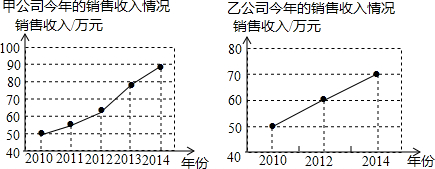
    A．甲公司近年的销售收入增长速度比乙公司快
    B．乙公司近年的销售收入增长速度比甲公司快
    C．甲、乙两公司近年的销售收入增长速度一样快
    D．不能确定甲、乙两公司近年销售收入增长速度的快慢

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    14．若a，b为有理数，且（$\sqrt{3}$+$\sqrt{2}$）2-$\frac{\sqrt{3}+\sqrt{2}}{\sqrt{3}}$=a+b$\sqrt{6}$，则a=4，b=$\frac{5}{3}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．若$\sqrt{\frac{x}{y-1}}$=$\frac{\sqrt{x}}{\sqrt{y-1}}$，求x，y的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    18．已知4×23m•44m=29，求m的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．阅读下列材料，并用相关的思想方法解决问题．
    计算：3.1468×7.1468-0.14682．
    解：设0.1468=a，∴原式=（a+3）（a+7）-a2=a2+10a+21-a2=10a+21
    把a=0.1468代入，∴原式=10×0.1468+21=22.468．
    问题：
    （1）计算：（1-$\frac{1}{2}$-$\frac{1}{3}$-$\frac{1}{4}$）×（$\frac{1}{2}$+$\frac{1}{3}$+$\frac{1}{4}$+$\frac{1}{5}$）-（1-$\frac{1}{2}$-$\frac{1}{3}$-$\frac{1}{4}$-$\frac{1}{5}$）×（$\frac{1}{2}$+$\frac{1}{3}$+$\frac{1}{4}$）．
    （2）若M=56789×56786，N=56788×56787，试比较M，N的大小．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．背景介绍：勾股定理是几何学中的明珠，充满着魅力．千百年来，人们对它的证明趋之若骛，其中有著名的数学家，也有业余数学爱好者．向常春在1994年构造发现了一个新的证法．
    小试牛刀：把两个全等的直角三角形如图1放置，其三边长分别为a、b、c．显然，
    ∠DAB=∠B=90°，AC⊥DE．请用a、b、c分别表示出梯形ABCD、四边形AECD、△EBC的面积，再探究这三个图形面积之间的关系，可得到勾股定理：

    S梯形ABCD=$\frac{1}{2}$a（a+b），
    S△ABC=$\frac{1}{2}$b（a-b），
    S四边形AECD=$\frac{1}{2}$c2，
    则它们满足的关系式为$\frac{1}{2}$a（a+b）=$\frac{1}{2}$b（a-b）+$\frac{1}{2}$c2经化简，可得到勾股定理．
    知识运用：
    （1）如图2，铁路上A、B两点（看作直线上的两点）相距40千米，C、D为两个村庄（看作两个点），AD⊥AB，BC⊥AB，垂足分别为A、B，AD=25千米，BC=16千米，则两个村庄的距离为41千米（直接填空）；
    （2）在（1）的背景下，若AB=40千米，AD=24千米，BC=16千米，要在AB上建造一个供应站P，使得PC=PD，请用尺规作图在图2中作出P点的位置并求出AP的距离．
    知识迁移：借助上面的思考过程与几何模型，求代数式$\sqrt{{x}^{2}+9}$$+\sqrt{（16-x）^{2}+81}$的最小值（0＜x＜16）

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    20．甲乙两名运动员在长50米的游泳池两边同时开始相向游泳，甲游50米要36秒，乙游50米要30秒，略去转身时间不计，在6分钟内二人相遇11次．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    1．如图，在Rt△BAD中，延长斜边BD到点C，使DC=$\frac{1}{2}BD$，连接AC，若tanB=$\frac{5}{3}$，求tan∠CAD的值．

    查看答案和解析>>

    同步练习册答案