
| A. | 30° | B. | 40° | C. | 50° | D. | 60° |
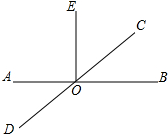
分析 首先根据EO⊥AB,可得∠EOB=90°;然后根据∠COB=∠EOB-∠EOC,求出∠COB的度数;最后根据对顶角的性质,求出∠AOD的度数即可.
解答 解:∵EO⊥AB,
∴∠EOB=90°.
又∵∠EOC=30°,
∴∠COB=∠EOB-∠EOC=90°-40°=50°,
∵∠AOD=∠COB,
∴∠AOD=50°.
故选:C.
点评 (1)此题主要考查了垂线的性质和应用,要熟练掌握,解答此题的关键是要明确垂线的性质:在平面内,过一点有且只有一条直线与已知直线垂直.
(2)此题还考查了对顶角和邻补角的特征和应用,要熟练掌握,解答此题的关键是要明确:①有一个公共顶点,并且一个角的两边分别是另一个角的两边的反向延长线,具有这种位置关系的两个角,互为对顶角.②补角互补,即和为180°.


科目:初中数学 来源: 题型:选择题
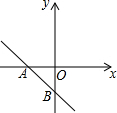 如图,一次函数y=(m-1)x-3+m的图象分别于x轴、y轴的负半轴相交于点A、B,则m的取值范围是( )
如图,一次函数y=(m-1)x-3+m的图象分别于x轴、y轴的负半轴相交于点A、B,则m的取值范围是( )| A. | m>3 | B. | m<3 | C. | m>1 | D. | m<1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
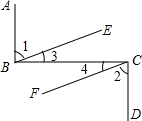 已知:如图AB⊥BC,BC⊥CD且∠1=∠2,试说明:BE∥CF.
已知:如图AB⊥BC,BC⊥CD且∠1=∠2,试说明:BE∥CF.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 了解某班学生对中国首辆月球车--“玉兔”的知晓情况 | |
| B. | 了解某市中学生每天体育锻炼的时间 | |
| C. | 了解某市市民对城市建设的满意度 | |
| D. | 了解南方人对雾霾危害的了解情况 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com