
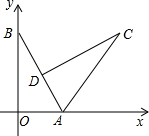
 如图,平面直角坐标系中,已知O为坐标原点,A(3,0),B(0,4).将Rt△AOB绕点A顺时针旋转得到Rt△ACD,旋转后点D恰好落在AB边上时,则D点的坐标为($\frac{6}{5}$,$\frac{12}{5}$).
如图,平面直角坐标系中,已知O为坐标原点,A(3,0),B(0,4).将Rt△AOB绕点A顺时针旋转得到Rt△ACD,旋转后点D恰好落在AB边上时,则D点的坐标为($\frac{6}{5}$,$\frac{12}{5}$). 分析 过点D作DE⊥OA,垂足为E,然后在Rt△AOB中,由勾股定理求得AB的长度,接下来再证明△AED∽△AOB,最后由相似三角形的性质求得AE、DE的长度,从而可求得点D的坐标.
解答 解:过点D作DE⊥OA,垂足为E.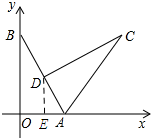
由点A、B的坐标可知;OA=3,OB=4.
在Rt△AOB中,由勾股定理得:AB=$\sqrt{O{A}^{2}+O{B}^{2}}$=5,
由旋转的性质可知:AD=3.
∵OB⊥OA,DE⊥OA,
∴DE∥OB.
∴△AED∽△AOB.
∴$\frac{DA}{AB}=\frac{AE}{AO}=\frac{ED}{OB}$,即$\frac{3}{5}=\frac{AE}{3}=\frac{ED}{4}$,
∴AE=$\frac{9}{5}$,ED=$\frac{12}{5}$,
∴OE=OA-AE=3-$\frac{9}{5}$=$\frac{6}{5}$,
∴点D的坐标为($\frac{6}{5}$,$\frac{12}{5}$).
点评 本题主要考查的是旋转的性质、相似三角形的性质和判定、勾股定理的应用,由相似三角形的性质求得AE、DE的长度是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
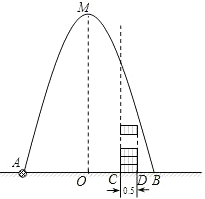 如图,在水平地面点A处有一网球发射器向空中发射网球,网球飞行路线是一条抛物线,在地面上落点为B,有人在直线AB上点C(靠点B一侧)竖直向上摆放若干个无盖的圆柱形桶.试图让网球落入桶内,已知AB=4米,AC=3米,网球飞行最大高度OM=5米,圆柱形桶的直径为0.5米,高为0.3米(网球的体积和圆柱形桶的厚度忽略不计).当竖直摆放圆柱形桶至少8个时,网球可以落入桶内.
如图,在水平地面点A处有一网球发射器向空中发射网球,网球飞行路线是一条抛物线,在地面上落点为B,有人在直线AB上点C(靠点B一侧)竖直向上摆放若干个无盖的圆柱形桶.试图让网球落入桶内,已知AB=4米,AC=3米,网球飞行最大高度OM=5米,圆柱形桶的直径为0.5米,高为0.3米(网球的体积和圆柱形桶的厚度忽略不计).当竖直摆放圆柱形桶至少8个时,网球可以落入桶内.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
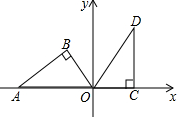 如图,直角坐标系中,Rt△DOC的直角边OC在x轴上,∠OCD=90°,OD=6,OC=3,现将△DOC绕原点O按逆时针方向旋转,得到△AOB,且点A在x轴上.
如图,直角坐标系中,Rt△DOC的直角边OC在x轴上,∠OCD=90°,OD=6,OC=3,现将△DOC绕原点O按逆时针方向旋转,得到△AOB,且点A在x轴上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
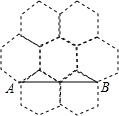 蜂巢的构造非常复杂,科学,如图是由7个全等的正六边形组成的网络,正六边形的顶点称为格点,△ABC的顶点都在格点上,设定AB边如图所示,则△ABC是直角三角形的个数有( )
蜂巢的构造非常复杂,科学,如图是由7个全等的正六边形组成的网络,正六边形的顶点称为格点,△ABC的顶点都在格点上,设定AB边如图所示,则△ABC是直角三角形的个数有( )| A. | 10个 | B. | 8个 | C. | 6个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
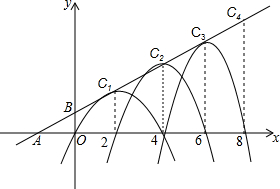 如图,在平面直角坐标系中,A(-2,0),B(0,1),有一组抛物线ln,它们的顶点Cn(xn.yn)在直线AB上,并且经过(xn+1,0),当n=1,2,3,4…时,xn=2,4,6,8…根据上述规律,写出抛物线l7的表达式为y=-$\frac{23}{2}$(x-2)2+$\frac{23}{2}$或y=-$\frac{23}{2}$x2+46x-$\frac{69}{2}$.
如图,在平面直角坐标系中,A(-2,0),B(0,1),有一组抛物线ln,它们的顶点Cn(xn.yn)在直线AB上,并且经过(xn+1,0),当n=1,2,3,4…时,xn=2,4,6,8…根据上述规律,写出抛物线l7的表达式为y=-$\frac{23}{2}$(x-2)2+$\frac{23}{2}$或y=-$\frac{23}{2}$x2+46x-$\frac{69}{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com