
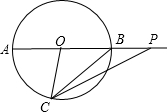
 如图,线段AB是⊙O的直径,点C在圆上,∠AOC=80°,点P是线段AB延长线上的一动点,连接PC,则∠APC的度数是30度(写出一个即可).
如图,线段AB是⊙O的直径,点C在圆上,∠AOC=80°,点P是线段AB延长线上的一动点,连接PC,则∠APC的度数是30度(写出一个即可).  冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
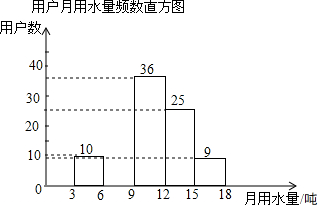 水利部确定每年的3月22日至28日为“中国水周”(1994年以前为7月1日至7日),从1991年起,我国还将每年5月的第二周作为城市节约用水宣传周.某社区为了进一步提高居民珍惜水、保护水和水忧患意识,提倡节约用水,从本社区5000户家庭中随机抽取100户,调查他们家庭每月的平均用水量,并将调查的结果绘制成如下的两幅不完整的统计图表:
水利部确定每年的3月22日至28日为“中国水周”(1994年以前为7月1日至7日),从1991年起,我国还将每年5月的第二周作为城市节约用水宣传周.某社区为了进一步提高居民珍惜水、保护水和水忧患意识,提倡节约用水,从本社区5000户家庭中随机抽取100户,调查他们家庭每月的平均用水量,并将调查的结果绘制成如下的两幅不完整的统计图表:| 用户月用水量频数分布表 | ||
| 平均用水量(吨) | 频数 | 频率 |
| 3~6吨 | 10 | 0.1 |
| 6~9吨 | m | 0.2 |
| 9~12吨 | 36 | 0.36 |
| 12~15吨 | 25 | n |
| 15~18吨 | 9 | 0.09 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
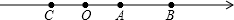 如图,点A、B、C都是数轴上的点,点B、C到点A的距离相等,若点A、B表示的数分别是2,$\sqrt{19}$,则点C表示的数为( )
如图,点A、B、C都是数轴上的点,点B、C到点A的距离相等,若点A、B表示的数分别是2,$\sqrt{19}$,则点C表示的数为( )| A. | 2-$\sqrt{19}$ | B. | $\sqrt{19}$-2 | C. | 4-$\sqrt{19}$ | D. | $\sqrt{19}$-4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{6}$ | B. | $\sqrt{9}$ | C. | $\sqrt{12}$ | D. | $\sqrt{18}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com