
分析 (1))①如图1中,画出图形,即可判断直线l1与l2与图形W成“$\sqrt{2}$相关”的直线.
②符合题意的直线如图2中所示.夹在直线a和b或c和d之间的(含直线a,b,c,d)都是符合题意的.
③如图3中,设符合题意的直线的解析式为 y=$\sqrt{3}$x+b,由题意可知符合题意的临界直线分别经过点(-1,1),(1,-1).分别代入可求出b1=1+$\sqrt{3}$,b2=-1-$\sqrt{3}$,由此即可解决问题.
(2)如图4中,⊙K与直线交于点A、B,直线与x轴交于点D(-3,0),作KC⊥AB于C.假设AB=3,求出DK,再根据对称性即可解决问题.
解答 解:(1)①如图1中,直线l1与l2图形W成“$\sqrt{2}$相关”的直线.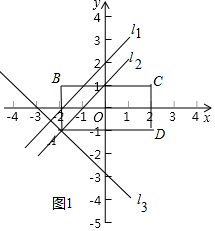
故答案为l1和l2.
②符合题意的直线如图2中所示.夹在直线a和b或c和d之间的(含直线a,b,c,d)都是符合题意的.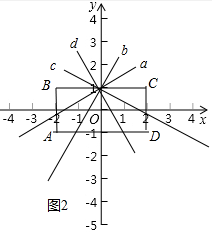
③如图3中,设符合题意的直线的解析式为 y=$\sqrt{3}$x+b,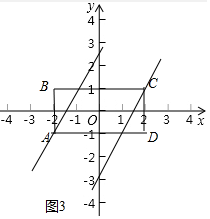
由题意可知符合题意的临界直线分别经过点(-1,1),(1,-1).
分别代入可求出b1=1+$\sqrt{3}$,b2=-1-$\sqrt{3}$,
∴-1-$\sqrt{3}$≤yQ≤1+$\sqrt{3}$.
(2)如图4中,⊙K与直线交于点A、B,直线与x轴交于点D(-3,0),作KC⊥AB于C.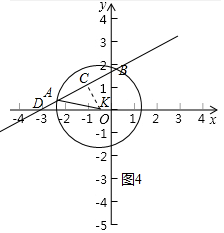
在Rt△AKC中,∵AC=BC=$\frac{3}{2}$,KA=2,
∴CO=$\sqrt{K{A}^{2}-A{C}^{2}}$=$\sqrt{{2}^{2}-(\frac{3}{2})^{2}}$=$\frac{\sqrt{7}}{2}$,
在Rt△CDK,∵∠CDO=30°,
∴DK=2CO=$\sqrt{2}$,
根据对称性可知,当-3-$\sqrt{7}$≤xK≤-3+$\sqrt{7}$时,若直线y=$\frac{\sqrt{3}}{3}$x+$\sqrt{3}$与图形 W成“3相关”.
点评 本题考查圆综合题、一次函数的应用、勾股定理,解直角三角形等知识,综合性比较强,理解题意是解题的关键,属于中考创新题目.


科目:初中数学 来源: 题型:解答题
 在平面直角坐标系xOy中,一次函数的图象经过点A(4,1)与点B(0,5).
在平面直角坐标系xOy中,一次函数的图象经过点A(4,1)与点B(0,5).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,已知弧BC的半径为3,圆心角为120°,圆心为点A.D为弧BC上一动点,以D为旋转中心,将点B顺时针旋转120°得到点E.若点D从B运动到点C,则点E的运动路径长为( )
如图,已知弧BC的半径为3,圆心角为120°,圆心为点A.D为弧BC上一动点,以D为旋转中心,将点B顺时针旋转120°得到点E.若点D从B运动到点C,则点E的运动路径长为( )| A. | 3$\sqrt{3}$π | B. | 2$\sqrt{3}$π | C. | 12 | D. | 9 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com