
分析 先利用平方差公式和立方和、立方差公式得到原式=y•[$\frac{(\sqrt{x}+\sqrt{y})(x-\sqrt{xy}+y)}{y(\sqrt{x}+\sqrt{y})(\sqrt{x}-\sqrt{y})}$-$\frac{x+\sqrt{xy}+y}{(\sqrt{x}-\sqrt{y})(x+\sqrt{xy}+y)}$],再约分后进行通分,然后再约分即可.
解答 解:原式=y•[$\frac{(\sqrt{x}+\sqrt{y})(x-\sqrt{xy}+y)}{y(\sqrt{x}+\sqrt{y})(\sqrt{x}-\sqrt{y})}$-$\frac{x+\sqrt{xy}+y}{(\sqrt{x}-\sqrt{y})(x+\sqrt{xy}+y)}$]
=y•[$\frac{x-\sqrt{xy}+y}{y(\sqrt{x}-\sqrt{y})}$-$\frac{1}{\sqrt{x}-\sqrt{y}}$]
=y•$\frac{x-\sqrt{xy}+y-y}{y(\sqrt{x}-\sqrt{y})}$
=$\frac{\sqrt{x}(\sqrt{x}-\sqrt{y})}{\sqrt{x}-\sqrt{y}}$
=$\sqrt{x}$.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
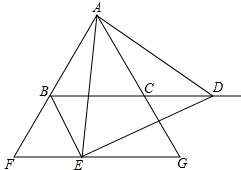 如图:△ABC是等边三角形,点D是射线BC上的一个动点(点D不与点B、C重合),△ADE是以AD为边的等边三角形,过点E作BC的平行线,分别交射线AB、AC于点F、G,连接BE.
如图:△ABC是等边三角形,点D是射线BC上的一个动点(点D不与点B、C重合),△ADE是以AD为边的等边三角形,过点E作BC的平行线,分别交射线AB、AC于点F、G,连接BE.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
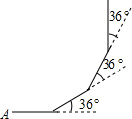 如图,小明从A点出发,沿直线前进12米后向左转36°,再沿直线前进12米,又向左转36°…照这样走下去,他第一次回到出发地A点时,一共走了120米.
如图,小明从A点出发,沿直线前进12米后向左转36°,再沿直线前进12米,又向左转36°…照这样走下去,他第一次回到出发地A点时,一共走了120米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
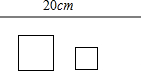 刘老师在数学课上给出了一个情景:如图,将一根长为20cm的铁丝剪成两段,以每一段为周长各围成一个正方形.
刘老师在数学课上给出了一个情景:如图,将一根长为20cm的铁丝剪成两段,以每一段为周长各围成一个正方形.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
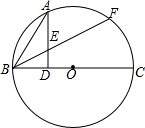 如图,BC是⊙O的直径,AD⊥BC于D,$\widehat{AB}$=$\widehat{AF}$,BF交AD于E
如图,BC是⊙O的直径,AD⊥BC于D,$\widehat{AB}$=$\widehat{AF}$,BF交AD于E查看答案和解析>>
科目:初中数学 来源: 题型:解答题
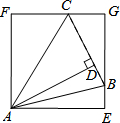 如图,△ABC中,∠BAC=45°,AD⊥BC,BD=1,CD=3,将△ABD沿AB折叠得到△ABE,将△ACD沿AC折叠得到△ACF,延长EB和FC交于点G.
如图,△ABC中,∠BAC=45°,AD⊥BC,BD=1,CD=3,将△ABD沿AB折叠得到△ABE,将△ACD沿AC折叠得到△ACF,延长EB和FC交于点G.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
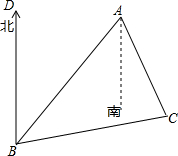 如图所示,B处在A处的南偏西45°方向上,C处在A处的南偏东30°方向,C处在B处的北偏东85°,求∠ACB是多少度?(提示:在三角形ABC中,∠BAC+∠ABC+∠ACB=180°)
如图所示,B处在A处的南偏西45°方向上,C处在A处的南偏东30°方向,C处在B处的北偏东85°,求∠ACB是多少度?(提示:在三角形ABC中,∠BAC+∠ABC+∠ACB=180°)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com