
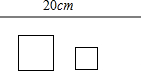
 刘老师在数学课上给出了一个情景:如图,将一根长为20cm的铁丝剪成两段,以每一段为周长各围成一个正方形.
刘老师在数学课上给出了一个情景:如图,将一根长为20cm的铁丝剪成两段,以每一段为周长各围成一个正方形.分析 (1)根据正方形的周长公式得到其边长,然后计算其面积即可;
(2)假设存在这样的x值,根据面积相差5cm2,列出关于x的方程,然后解方程.
解答 解:(1)依题意得,$\frac{x}{4}$×$\frac{x}{4}$-$\frac{20-x}{4}$×$\frac{20-x}{4}$=$\frac{{x}^{2}-(20-x)^{2}}{16}$=$\frac{(x+20-x)(x-20+x)}{16}$=$\frac{5}{2}$x-25.
即这两个正方形的面积之差为:$\frac{5}{2}$x-25.
(2)假设存在这样的x值,使两个正方形的面积刚好相差5cm2.则
$\frac{5}{2}$x-25=5,
解得x=12.符合题意.
即当x=12时,这两个正方形的面积刚好相差5cm2.
点评 本题考查了平方差公式.解题的关键是熟悉正方形的周长、面积公式.


 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案科目:初中数学 来源: 题型:填空题
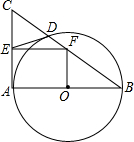 如图所示,以Rt△ABC的直角边AB为直径⊙O交BC边于D点,过D点作⊙O的切线交AC边于E点,又过E点作EF∥AB交BC于F点.若AB=20,CD=9,则OF=$\frac{15}{2}$.
如图所示,以Rt△ABC的直角边AB为直径⊙O交BC边于D点,过D点作⊙O的切线交AC边于E点,又过E点作EF∥AB交BC于F点.若AB=20,CD=9,则OF=$\frac{15}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
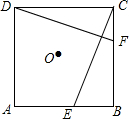 如图,E、F分别是正方形ABCD的边AB、BC上的点,且BE=CF,连接CE、DF,将△DCF绕着正方形的中心O按顺时针方向旋转到△CBE的位置,则旋转角为( )
如图,E、F分别是正方形ABCD的边AB、BC上的点,且BE=CF,连接CE、DF,将△DCF绕着正方形的中心O按顺时针方向旋转到△CBE的位置,则旋转角为( )| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
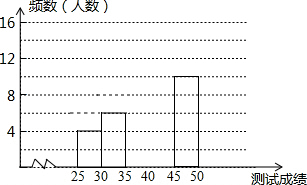 为了提高学生书写汉字的能力.增强保护汉字的意识,我区举办了“汉字听写大赛”,经选拔后有50名学生参加决赛,这50名学生同时听写50个汉字,若每正确听写出一个汉字得1分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表:
为了提高学生书写汉字的能力.增强保护汉字的意识,我区举办了“汉字听写大赛”,经选拔后有50名学生参加决赛,这50名学生同时听写50个汉字,若每正确听写出一个汉字得1分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表:| 组别 | 成绩x分 | 频数(人数) |
| 第1组 | 25≤x<30 | 4 |
| 第2组 | 30≤x<35 | 6 |
| 第3组 | 35≤x<40 | 14 |
| 第4组 | 40≤x<45 | a |
| 第5组 | 45≤x<50 | 10 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,将矩形ABCO放在直角坐标系中,其中顶点B的坐标为(10,8),E是BC边上一点,将△ABE沿AE折叠,点B刚好与OC边上点D重合,过点E的反比例函数y=$\frac{k}{x}$的图象与边AB交于点F,则线段AF的长为( )
如图,将矩形ABCO放在直角坐标系中,其中顶点B的坐标为(10,8),E是BC边上一点,将△ABE沿AE折叠,点B刚好与OC边上点D重合,过点E的反比例函数y=$\frac{k}{x}$的图象与边AB交于点F,则线段AF的长为( )| A. | $\frac{15}{4}$ | B. | 2 | C. | $\frac{15}{8}$ | D. | $\frac{3}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com