
分析 分别求得第一、二、三…八次变换后的坐标,得到每8次循环一次.则2013÷8=251…5即可求得结果.
解答 解:由题意第一次旋转后的坐标为($\frac{\sqrt{2}}{2}$,$\frac{\sqrt{2}}{2}$),
第二次旋转后的坐标为(0,-1),
第三次旋转后的坐标为(-$\frac{\sqrt{2}}{2}$,$\frac{\sqrt{2}}{2}$),
第四次旋转后的坐标为(1,0),
第五次旋转后的坐标为(-$\frac{\sqrt{2}}{2}$,-$\frac{\sqrt{2}}{2}$),
第六次旋转后的坐标为(0,1),
第七次旋转后的坐标为($\frac{\sqrt{2}}{2}$,-$\frac{\sqrt{2}}{2}$),
第八次旋转后的坐标为(-1,0)
因为2013÷8=251…5,
所以把点A经过连续2013次这样的变换得到的点A2013的坐标是(-$\frac{\sqrt{2}}{2}$,-$\frac{\sqrt{2}}{2}$).
故答案是:(-$\frac{\sqrt{2}}{2}$,-$\frac{\sqrt{2}}{2}$).
点评 本题考查了坐标与图形变化-旋转.解答此类找规律的问题的关键是仔细分析题中所给的特征得到规律,再把这个规律应用于解题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
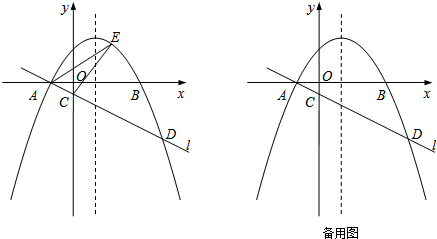
 如图所示,抛物线y=ax2+bx+4与x轴交于A,B两点,与y轴交于C点,且A(-2,0)、B(4,0),其原点为D,连接BD,点P是线段BD上的一个动点(不与B、D重合),过点P作y轴的垂线,垂足为E,连接BE.
如图所示,抛物线y=ax2+bx+4与x轴交于A,B两点,与y轴交于C点,且A(-2,0)、B(4,0),其原点为D,连接BD,点P是线段BD上的一个动点(不与B、D重合),过点P作y轴的垂线,垂足为E,连接BE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
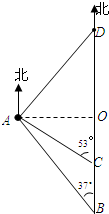 如图,一艘货船以每小时48海里的速度从港口B出发,沿正北方向航行.在港口B处时,测得灯塔A处在B处的北偏西37°方向上,航行至C处,测得A处在C处的北偏西53°方向上,且A、C之间的距离是45海里.在货船航行的过程中,求货船与灯塔A之间的最短距离及B、C之间的距离;若货船从港口B出发2小时后到达D,求A、D之间的距离.
如图,一艘货船以每小时48海里的速度从港口B出发,沿正北方向航行.在港口B处时,测得灯塔A处在B处的北偏西37°方向上,航行至C处,测得A处在C处的北偏西53°方向上,且A、C之间的距离是45海里.在货船航行的过程中,求货船与灯塔A之间的最短距离及B、C之间的距离;若货船从港口B出发2小时后到达D,求A、D之间的距离.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com