
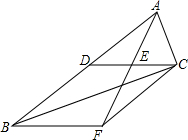
 如图,CD是△ABC的中线,点E是AF的中点,CF∥AB.
如图,CD是△ABC的中线,点E是AF的中点,CF∥AB.分析 (1)根据中点的性质,可得AE与EF的关系,根据平行的性质,可得内错角相等,根据全等三角形的判定与性质,可得CF与DA的关系,根据等量代换,可得答案;
(2)根据一组对边平行且相等的四边形是平行四边形,可得四边形BFCD的形状,根据直角三角形的性质,可得BD=CD,根据菱形的判定,可得答案;
解答 (1)证明∵AE是DC边上的中线,
∴AE=FE,
∵CF∥AB,
∴∠ADE=∠CFE,∠DAE=∠CFE.
在△ADE和△FCE中,
$\left\{\begin{array}{l}{∠ADE=∠CFE}\\{∠DAE=∠CFE}\\{AE=FE}\end{array}\right.$,
∴△ADE≌△FCE(AAS),
∴CF=DA.
(2)∵CD是△ABC的中线,
∴D是AB的中点,
∴AD=BD,
∵△ADE≌△FCE,
∴AD=CF,
∴BD=CF,
∵AB∥CF,
∴BD∥CF,
∴四边形BFCD是平行四边形,
∵∠ACB=90°,
∴△ACB是直角三角形,
∴CD=$\frac{1}{2}$AB,
∵BD=$\frac{1}{2}$AB,
∴BD=CD,
∴四边形BFCD是菱形.
点评 本题考查了四边形综合题,(1)利用了全等三角形的判定与性质,(2)利用了直角三角形的性质,菱形的判定分析.


 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:初中数学 来源: 题型:解答题
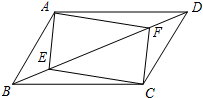 如图,在四边形ABCD中,E、F分别为对角线BD上的两点,且BE=DF.
如图,在四边形ABCD中,E、F分别为对角线BD上的两点,且BE=DF.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
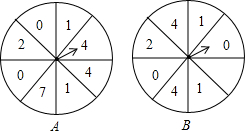 某天,小明和小华利用“争1点”的游戏来预测一场足球比赛的冠军.如图,两个可以自由转动的转盘A,B,每个转盘被分成8个相等的扇形,其规则如下:①小明自由转动转盘A,同时小华自由转动转盘B;②转盘停止后,指针指向几就顺时针走几格,得到一个数字(若转盘A中指针指向2,则按顺时针方向走2格得到数字1);③若最终得到的数字是1,则自己所支持的球队称为预测冠军(若双方都得到1,则重新开始).这个游戏对双方公平吗?请说明理由.
某天,小明和小华利用“争1点”的游戏来预测一场足球比赛的冠军.如图,两个可以自由转动的转盘A,B,每个转盘被分成8个相等的扇形,其规则如下:①小明自由转动转盘A,同时小华自由转动转盘B;②转盘停止后,指针指向几就顺时针走几格,得到一个数字(若转盘A中指针指向2,则按顺时针方向走2格得到数字1);③若最终得到的数字是1,则自己所支持的球队称为预测冠军(若双方都得到1,则重新开始).这个游戏对双方公平吗?请说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
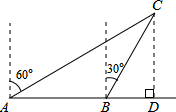 如图,一渔船由西往东航行,在A点测得海岛C位于北偏东60°的方向,前进40海里到达B点,此时,测得海岛C位于北偏东30°的方向,则海岛C到航线AB的距离CD是( )
如图,一渔船由西往东航行,在A点测得海岛C位于北偏东60°的方向,前进40海里到达B点,此时,测得海岛C位于北偏东30°的方向,则海岛C到航线AB的距离CD是( )| A. | 20海里 | B. | 40海里 | C. | 20$\sqrt{3}$海里 | D. | 40$\sqrt{3}$海里 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,抛物线y=ax2+bx+4与x轴交于A,B两点,与y轴交于C点,且A(-2,0)、B(4,0),其原点为D,连接BD,点P是线段BD上的一个动点(不与B、D重合),过点P作y轴的垂线,垂足为E,连接BE.
如图所示,抛物线y=ax2+bx+4与x轴交于A,B两点,与y轴交于C点,且A(-2,0)、B(4,0),其原点为D,连接BD,点P是线段BD上的一个动点(不与B、D重合),过点P作y轴的垂线,垂足为E,连接BE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
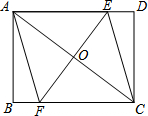 如图,矩形ABCD中,对角线AC的垂直平分线交AD、BC于点E、F,AC与EF交于点O,连结AF、CE.
如图,矩形ABCD中,对角线AC的垂直平分线交AD、BC于点E、F,AC与EF交于点O,连结AF、CE.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com